
【题目】以下命题,①若实数![]() ,则
,则![]() .
.
②归纳推理是由特殊到一般的推理,而类比推理是由特殊到特殊的推理;
③在回归直线方程![]() 中,当变量
中,当变量![]() 每增加一个单位时,变量
每增加一个单位时,变量![]() 一定增加0.2单位.
一定增加0.2单位.
④“若![]() ,则复数
,则复数![]() ”类比推出“若
”类比推出“若![]() ,则
,则![]() ”;
”;
正确的个数是( )
A. 1B. 2C. 3D. 4
科目:高中数学 来源: 题型:
【题目】如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.
(1)求证:EF⊥BC;
(2)求二面角E-BF-C的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理财公司有两种理财产品A和B,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品A
投资结果 | 获利40% | 不赔不赚 | 亏损20% |
概率 |
|
|
|
产品B
投资结果 | 获利20% | 不赔不赚 | 亏损10% |
概率 | p |
| q |
注:p>0,q>0
(1)已知甲、乙两人分别选择了产品A和产品B投资,如果一年后他们中至少有一人获利的概率大于![]() ,求实数p的取值范围;
,求实数p的取值范围;
(2)若丙要将家中闲置的10万元人民币进行投资,以一年后投资收益的期望值为决策依据,则选用哪种产品投资较理想?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为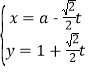 (
(![]() 为参数,
为参数,![]() ),以坐标原点为极点,以
),以坐标原点为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点(
两点(![]() 在
在![]() 之间),且
之间),且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农产品从5月1日起开始上市,通过市场调查,得到该农产品种植成本Q(单位:元/![]() )与上市时间t(单位:天)的数据如下表:
)与上市时间t(单位:天)的数据如下表:
t | 50 | 110 | 250 |
Q | 150 | 108 | 150 |
(1)根据上表数据,从下列函数中选取一个函数描述该农产品种植成本Q与上市时间t的变化关系,并求出函数关系式:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)利用你选取的函数,求该农产品种植成本最低时的上市时间及最低种植成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品促销活动设计了一个摸奖游戏:在一个口袋中装有4个红球和6个白球,这些球除颜色外完全相同,顾客一次从中摸出3个球,若3个都是白球则无奖励,若有1个红球则奖励10元购物券,若有2个红球则奖励20元购物券,若3个都是红球则奖励30元购物券.
(Ⅰ)求中奖的概率;
(Ⅱ)求顾客摸奖一次获得购物券奖励的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(原创题)已知点![]() 是椭圆
是椭圆![]() 和抛物线
和抛物线![]() 的公共焦点,
的公共焦点,![]() 是椭圆的长轴的两个端点,点
是椭圆的长轴的两个端点,点![]() 是
是![]() 与
与![]() 在第二象限的交点,且
在第二象限的交点,且![]() .
.
(I) 求椭圆![]() 的方程;
的方程;
(II) 点![]() 为直线
为直线![]() 上的动点,过点
上的动点,过点![]() 作抛物线
作抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .直线
.直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设△
两点,设△![]() 的面积为
的面积为![]() ,△
,△![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com