练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．直线mx-y-m+2=0恒过定点A，若直线l过点A且与2x+y-2=0平行，则直线l的方程为（　　）
    A．2x+y-4=0B．2x+y+4=0C．x-2y+3=0D．x-2y-3=0

    分析 求出A的坐标，求出直线l的斜率，从而求出直线l的方程即可．

    解答 解：由mx-y-m+2=0，得：y-2=m（x-1），
    故直线mx-y-m+2=0恒过定点A（1，2），
    直线2x+y-2=0的斜率是：k=-2，
    故直线l的方程是：y-2=-2（x-1），
    整理得：2x+y-4=0，
    故选：A．

    点评 本题考查了求直线方程问题，考查直线的平行关系，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

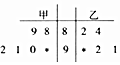    17．在某校组织的“共筑中国梦”竞赛活动中，甲、乙两班各有6位选手参赛，在第一轮笔试环节中，评委将他们的笔试成绩作为样本数据，绘制成如图所示的茎叶图．为了增加结果的神秘感，主持人暂时没有公布甲、乙两班最好一位选手的成绩．
    （Ⅰ）求乙班总分超过甲班的概率；
    （Ⅱ）主持人最后宣布：甲班第六位选手的得分是90分，乙班第六位选手的得分是97分．请你从平均分和方差的角度来分析两个班的选手的情况．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知两个命题p：?x∈R，sinx+cosx＞m恒成立，q：?x∈R，y=（2m2-m）x为增函数．若p∨q为真命题，p∧q为假命题，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

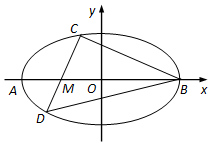    15．在平面直角坐标系xOy中，椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，两个顶点分别为A（-a，0），B（a，0），点M（-1，0），且3$\overrightarrow{AM}$=$\overrightarrow{MB}$，过点M斜率为k（k≠0）的直线交椭圆E于C，D两点，且点C在x轴上方．
    （1）求椭圆E的方程；
    （2）若BC⊥CD，求k的值；
    （3）记直线BC，BD的斜率分别为k1，k2，求证：k1k2为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知α是三角形的内角，且sinα+cosα=$\frac{1}{5}$．
    （1）求cos2α的值；
    （2）把$\frac{1}{sinα•cosα}$用tanα表示出来，并求其值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知集合A={x|-2≤x≤5}，B={x|m+1≤x≤2m-1}
    （1）若B=∅，求m的取值范围；
    （2）若B⊆A，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

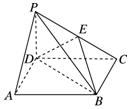    19．如图所示，在四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD是正方形，PD=AB=2，E为PC中点．求二面角E-BD-P的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．下列说法中，正确的是（　　）
    A．经过不同的三点有且只有一个平面
    B．分别在两个平面内的两条直线是异面直线
    C．垂直于同一个平面的两条直线平行
    D．垂直于同一个平面的两个平面平行

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．等差数列{an}中，a1=2，a5=a4+2，则a3=（　　）
    A．4B．10C．8D．6

    查看答案和解析>>

    同步练习册答案