
【题目】设函数![]() ,曲线y=f(x)在点(1, f(1))处的切线方程为y=e(x-1)+2.
,曲线y=f(x)在点(1, f(1))处的切线方程为y=e(x-1)+2.
(1)求![]() (2)证明:
(2)证明: ![]()
【答案】(I)![]() ;(II)详见解析.
;(II)详见解析.
【解析】试题分析:(1)根据求导法则求出原函数的导函数,由某点的导数是在该点的切线的斜率,结合切线方程以及该点的函数值,将函数值和切线斜率代入原函数和导函数可求得参数值;(2)由(1 )可得![]() 的解析式,
的解析式, ![]() 为多项式,对要证的不等式进行变形,使之成为两个函数的大小关系式,再分别利用导函数求出两函数在定义域内的最值,可证得两函数的大小关系,进而证得.
为多项式,对要证的不等式进行变形,使之成为两个函数的大小关系式,再分别利用导函数求出两函数在定义域内的最值,可证得两函数的大小关系,进而证得.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]() .
.
由题意可得![]() ,
, ![]() .故
.故![]() ,
, ![]() .
.
(2)证明:由(1)知, ![]() ,
,
从而![]() 等价于
等价于![]() .
.
设函数![]() ,则
,则![]() .
.
所以当![]() ,
, ![]() ;
;
当![]() 时,
时, ![]() .
.
故![]() 在
在![]() 上单调递减,
上单调递减, ![]() 上单调递增,从而
上单调递增,从而![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
设函数![]() ,则
,则![]() .
.
所以当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .故
.故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,从而
上单调递减,从而![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
综上,当![]() 时,
时, ![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,ABCD是块矩形硬纸板,其中AB=2AD,AD=![]() ,E为DC的中点,将它沿AE折成直二面角D-AE-B.
,E为DC的中点,将它沿AE折成直二面角D-AE-B.
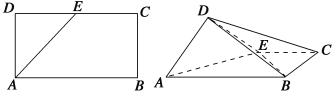
(1)求证:AD⊥平面BDE;
(2)求二面角B-AD-E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对高一年级学生寒假参加社区服务的次数进行了统计,随机抽取了![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:

(1)求表中![]() 的值和频率分布直方图中
的值和频率分布直方图中![]() 的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
(2)如果用分层抽样的方法从样本服务次数在![]() 和
和![]() 的人中共抽取6人,再从这6人中选2人,求2人服务次数都在
的人中共抽取6人,再从这6人中选2人,求2人服务次数都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(4, 0),B(2, 2),C (6, 0),记△ABC的外接圆为⊙P.
(1)求⊙P的方程.
(2)对于线段PA上的任意一点G,是否存在以B为圆心的圆,在圆B上总能找到不同的两点E、F,满足![]() =
=![]() ,若存在,求圆B的半径
,若存在,求圆B的半径![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差![]() 与实验室每天每100颗种子浸泡后的发芽数
与实验室每天每100颗种子浸泡后的发芽数![]() ,作了初步处理,得到下表:
,作了初步处理,得到下表:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 9 |
发芽率 | 23 | 25 | 30 | 26 | 16 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均小于26”的概率;
均小于26”的概率;
(2)请根据3月1日至3月5日的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预报3月份昼夜温差为14度时实验室每天100颗种子浸泡后的发芽(取整数值).
,并预报3月份昼夜温差为14度时实验室每天100颗种子浸泡后的发芽(取整数值).
附:回归方程![]() 中的斜率和截距最小二乘法估计公式分别为:
中的斜率和截距最小二乘法估计公式分别为: ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂有容量300吨的水塔一个,每天从早六点到晚十点供应生活和生产用水,已知:该厂生活用水每小时10吨,工业用水总量![]() (吨)与时间
(吨)与时间![]() (单位:小时,规定早晨六点时
(单位:小时,规定早晨六点时![]() )的函数关系为
)的函数关系为![]() ,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级, 进水量增加10吨.若某天水塔原有水100吨,在供应同时打开进水管.问该天进水量应选择几级,既能保证该厂用水(即水塔中水不空),又不会使水溢出?
,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级, 进水量增加10吨.若某天水塔原有水100吨,在供应同时打开进水管.问该天进水量应选择几级,既能保证该厂用水(即水塔中水不空),又不会使水溢出?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共13分)根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示
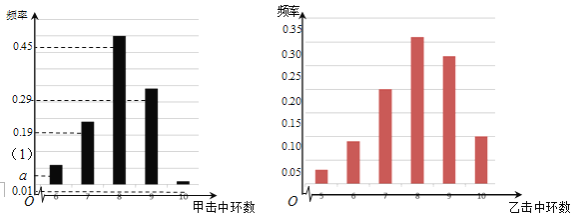
(1)求上图中![]() 的值;
的值;
(2)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);
(3)由上图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com