练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．一海豚在水池中（不考虑水的深度）自由游戏，已知水池的长为30m，宽为20m，则海豚嘴尖离池边超过4m的概率为$\frac{11}{25}$．

    分析 测度为面积，找出点离岸边不超过4m的点对应的图形的面积，并将其和长方形面积一齐代入几何概型计算公式进行求解．

    解答 解：如图所示：长方形面积为20×30，小长方形面积为22×12，
    阴影部分的面积为20×30-22×12，
    ∴海豚嘴尖离岸边不超过2m的概率为P=1-$\frac{22×12}{20×30}$=$\frac{11}{25}$．
    故答案为$\frac{11}{25}$．

    点评 本题考查几何概型，明确测度，正确求解面积是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．对于常数m、n，“mn＜0”是“方程mx2+ny2=10的曲线是双曲线”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

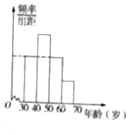    8．韩国民意调查机构“盖洛普韩国”2016年11月公布的民调结果显示，受“闺蜜门”时间影响，韩国总统朴槿惠的民意支持率持续下跌，在所调查的1000个对象中，年龄在[20，30）的群体有200人，支持率为0%，年龄在[30，40）和[40，50）的群体中，支持率均为3%；年龄在[50，60）和[60，70）的群体中，支持率分别为6%和13%，若在调查的对象中，除[20，30）的群体外，其余各年龄层的人数分布情况如频率分布直方图所示，其中最后三组的频数构成公差为100的等差数列．
    （1）依频率分布直方图求出图中各年龄层的人数
    （2）请依上述支持率完成下表：
                     年龄分布
    是否支持    		[30，40）和[40，50）[50，60）和[60，70） 合计
     支持152540
     不支持485275760
     合计500 300 800 
    根据表中的数据，能否在犯错误的概率不超过0.001的前提下认为年龄与支持率有关？
    附表：
     P（K2≥k） 0.150.10  0.05 0.0250.010 0.005 0.001 
     k 2.0722.076 3.841 5.024 6.635 7.879 10.828 
    （参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d    参考数据：125×33=15×275，125×97=25×485）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知点P是锐角△ABC所在平面内的动点，且满足$\overrightarrow{CP}•\overrightarrow{CB}=\overrightarrow{CA}•\overrightarrow{CB}$，给出下列四个命题：
    ①点P的轨迹是一条直线；
    ②$|\overrightarrow{CP}|=|\overrightarrow{CA}|$恒成立；
    ③$|\overrightarrow{CP}|≥|\overrightarrow{CA}|cosC$；
    ④存在点P使得$|\overrightarrow{PC}+\overrightarrow{PB}|=|\overrightarrow{CB}|$．
    则其中真命题的序号为（　　）
    A．①②B．③④C．①②④D．①③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知函数f（x）是定义域为R的奇函数，且当x＜0时xf'（x）+f（x）＜0，记a=3f（3），b=f（sin1）sin1，c=-2$\sqrt{2}f（-2\sqrt{2}）$，则a，b，c的大小关系式（　　）
    A．a＞c＞bB．c＞a＞bC．c＞b＞aD．a＞b＞c

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．△ABC是边长为2的正三角形，已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{AB}$=2$\overrightarrow{a}$，$\overrightarrow{AC}$=2$\overrightarrow{a}$+$\overrightarrow{b}$，给出下列四个结论．
    ①|$\overrightarrow{b}$|=1，②$\overrightarrow{a}$•$\overrightarrow{b}$=-1③$\overrightarrow{a}$⊥$\overrightarrow{b}$④（4$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{BC}$
    其中正确结论的序号是②④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

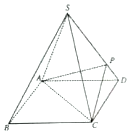    9．如图所示，四棱锥S-ABCD的底面是正方形，每条侧棱的长都是底面边长的$\sqrt{2}$倍，点P在侧棱SD上，且SP=3PD．
    （1）求证：AC⊥SD；
    （2）若$AB=\sqrt{2}$，求三棱锥D-ACP的体积；
    （3）侧棱SC上是否存在一点E，使得BE∥平面PAC，若存在，求$\frac{SE}{EC}$的值；若不存在，试说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知函数f（x）=$\left\{\begin{array}{l}{a^x}，x≥0\\ kx+1，x＜0\end{array}$，且0＜a＜1，k≠0，若函数g（x）=f（x）-k有两个零点，则实数k的取值范围为（0，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=ax2+lnx+1
    （1）讨论函数f（x）的单调性；
    （2）若对任意a∈（-2，-1）及x∈[1，2]，恒有ma-f（x）＞a2成立，求实数m的取值集合．

    查看答案和解析>>

    同步练习册答案