
分析 (1)①利用余弦定理可得cos∠F1PF2=$\frac{12}{2|P{F}_{1}||P{F}_{2}|}-1$,再利用椭圆的定义结合配方法求出|PF1|•|PF2|的最大值得答案;
②由①中过程可得|PF1|•|PF2|的取值范围;
③把$|\overrightarrow{P{F}_{1}}{|}^{2}+|\overrightarrow{P{F}_{2}}{|}^{2}$配方,转化为含有|PF1|•|PF2|的代数式求得最小值;
(2)由已知结合椭圆定义求出|PF1|,|PF2|,然后结合余弦定理求得椭圆的离心率;
(3)由(2)中求得的|PF2|,再由|PF2|≥a-c求得椭圆离心率的取值范围;
(4)由点P满足$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0,可得点P的轨迹是以F1F2为直径的圆,其方程为x2+y2=c2.进一步得到椭圆短轴的顶点在圆上或在圆的内部,可得b≤c,两边平方后结合隐含条件求得椭圆的离心率;
(5)由椭圆的对称性,结合△ABF1是锐角三角形,可得∠AF1F2<45°,即tan∠AF1F2<1,转化为a,b,c的不等式求得椭圆离心率的范围;
(6)先设出点M,N,A,B的坐标,然后表示出两斜率的关系,再由|k1|+|k2|的最小值为1,运用基本不等式的知识可得到当x0=0时可取到最小值,进而找到a,b,c的关系,求得离心率的值.
解答 解:(1)当a=2,b=$\sqrt{3}$时,椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$
①∵cos∠F1PF2=$\frac{|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}-|{F}_{1}{F}_{2}{|}^{2}}{2|P{F}_{1}||P{F}_{2}|}$=$\frac{(|P{F}_{1}|+|P{F}_{2}|)^{2}-2|P{F}_{1}||P{F}_{2}|-|{F}_{1}{F}_{2}{|}^{2}}{2|P{F}_{1}||P{F}_{2}|}$=$\frac{12}{2|P{F}_{1}||P{F}_{2}|}-1$,
故当|PF1||PF2|取得最大值时,cos∠F1PF2取最小值.
∵|PF1|+|PF2|=4,∴|PF2|=4-|PF1|,
∴|PF1|•|PF2|=|PF1|(4-|PF1|)=-(|PF1|-2)2+4,
∵1=2-1=a-c≤|PF1|≤a+c=2+1=3,
∴3≤-(|PF1|-2)2+4≤4,
∴|PF1|•|PF2|的最大值为4,最小值为3,
∴cos∠F1PF2的最小值是$\frac{1}{2}$;
②由①可得,|PF1|•|PF2|的取值范围是[3,4];
③∵$|\overrightarrow{P{F}_{1}}{|}^{2}+|\overrightarrow{P{F}_{2}}{|}^{2}$=(|PF1|+|PF2|)2-2|PF1|•|PF2|=16-2|PF1|•|PF2|,
由②知|PF1|•|PF2|的最大值为4,
∴$|\overrightarrow{P{F}_{1}}{|}^{2}+|\overrightarrow{P{F}_{2}}{|}^{2}$的最小值为16-8=8;
(2)∵椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$中,|PF1|+|PF2|=2a,
∴由|PF1|=2|PF2|,得|PF1|=$\frac{4}{3}a$,|PF2|=$\frac{2}{3}a$,
∵cos∠F1PF2=cos$\frac{π}{3}=\frac{1}{2}$,
∴|F1F2|2=|PF1|2+|PF2|2-2|PF1|•|PF2|cos∠F1PF2,
可得4c2=$\frac{16}{9}{a}^{2}+\frac{4}{9}{a}^{2}-2×\frac{4}{3}a×\frac{2}{3}a×\frac{1}{2}$=$\frac{4}{3}{a}^{2}$,
∴$\frac{{c}^{2}}{{a}^{2}}=\frac{1}{3}$,得椭圆的离心率e=$\frac{c}{a}=\frac{\sqrt{3}}{3}$;
(3)由(2)得,|PF2|=$\frac{2}{3}a$,
则$\frac{2}{3}a≥a-c$,解得$e=\frac{c}{a}≥\frac{1}{3}$,
又0<e<1,
∴椭圆离心率的取值范围是[$\frac{1}{3}$,1);
(4)∵点P满足$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0,
∴点P的轨迹是以F1F2为直径的圆,其方程为x2+y2=c2.
又∵椭圆上存在点P,满足$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0,
∴以F1F2为直径的圆与椭圆有公共点,
由此可得椭圆短轴的顶点在圆上或在圆的内部,
∴b≤c,即a2-c2≤c2,化简得a2≤2c2,解得$\frac{c}{a}≥\frac{\sqrt{2}}{2}$.
又0<e<1,
∴椭圆C的离心率e∈[$\frac{\sqrt{2}}{2}$,1);
(5)∵点F1、F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,
过F2且垂直于x轴的直线与椭圆交于A、B两点,
∴F1(-c,0),F2(c,0),A(c,$\frac{{b}^{2}}{a}$),B(c,-$\frac{{b}^{2}}{a}$),
∵△ABF1是锐角三角形,
∴∠AF1F2<45°,∴tan∠AF1F2<1,
∴$\frac{\frac{{b}^{2}}{a}}{2c}<1$,
整理得b2<2ac,
∴a2-c2<2ac,
两边同时除以a2,并整理,得e2+2e-1>0,
解得e>$\sqrt{2}$-1,或e<-$\sqrt{2}$-1,(舍),
又0<e<1,
∴椭圆的离心率e的取值范围是($\sqrt{2}$-1,1);
(6)设M(x0,y0),N(x0,-y0),A(-a,0),B(a,0),
则$\frac{{{x}_{0}}^{2}}{{a}^{2}}+\frac{{{y}_{0}}^{2}}{{b}^{2}}=1$,即有$\frac{{{y}_{0}}^{2}}{{a}^{2}-{{x}_{0}}^{2}}=\frac{{b}^{2}}{{a}^{2}}$,
k1=$\frac{{y}_{0}}{{x}_{0}+a}$,k2=$\frac{{y}_{0}}{a-{x}_{0}}$,
|k1|+|k2|=|$\frac{{y}_{0}}{{x}_{0}+a}$|+|$\frac{{y}_{0}}{a-{x}_{0}}$|≥2$\sqrt{\frac{{{y}_{0}}^{2}}{|{a}^{2}-{{x}_{0}}^{2}|}}=1$,
当且仅当$\frac{{y}_{0}}{{x}_{0}+a}=\frac{{y}_{0}}{a-{x}_{0}}$,即x0=0,y0=b时等号成立.
∴2$\sqrt{\frac{{{y}_{0}}^{2}}{|{a}^{2}-{{x}_{0}}^{2}|}}$=2•$\frac{b}{a}$=1,∴a=2b,
又∵a2=b2+c2,∴c=$\frac{\sqrt{3}}{2}a$,
∴e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$.
故答案为:(1)①$\frac{1}{2}$;②[3,4];③8;
(2)$\frac{\sqrt{3}}{3}$;(3)[$\frac{1}{3}$,1);(4)[$\frac{\sqrt{2}}{2}$,1);(5)($\sqrt{2}$-1,1);(6)$\frac{\sqrt{3}}{2}$.
点评 本题考查椭圆的简单性质,考查椭圆的定义,训练了涉及焦点三角形问题的解法,考查数学转化思想方法,考查学生的推理论证能力和数学求解能力,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}+\frac{y^2}{25}=1$ | B. | $\frac{x^2}{16}+\frac{y^2}{7}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{7}+\frac{y^2}{16}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
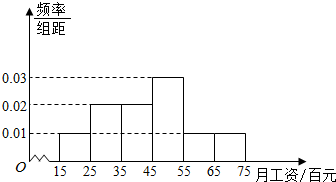
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥α,m⊥n,则n∥α | B. | 若m∥α,n∥α,则m∥n | ||
| C. | 若m,n与α所成的角相等,则m∥n | D. | 若m?α,m∥n,且n在平面α外,则n∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
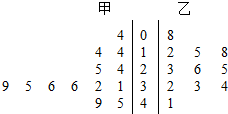 现今社会对食品安全的高度重视,各级政府加强了对食品安全的检查力度.某市工商质检局抽派甲、乙两个食品质量检查组到管辖区域内的商店进行食品质量检查.如图表示甲、乙两个检查组每天检查到的食品品种数的茎叶图,则甲、乙两个检查组每天检查到的食品种数的中位数的和是58.
现今社会对食品安全的高度重视,各级政府加强了对食品安全的检查力度.某市工商质检局抽派甲、乙两个食品质量检查组到管辖区域内的商店进行食品质量检查.如图表示甲、乙两个检查组每天检查到的食品品种数的茎叶图,则甲、乙两个检查组每天检查到的食品种数的中位数的和是58.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com