
科目:高中数学 来源: 题型:
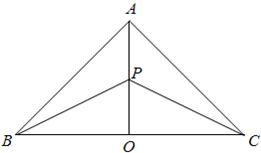 某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站.记P到三个村庄的距离之和为y.
某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站.记P到三个村庄的距离之和为y.查看答案和解析>>
科目:高中数学 来源: 题型:
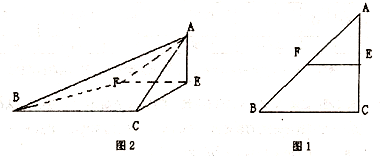 已知△ABC是腰长为2的等腰直角三角形(如图1),∠BCA=90°,在边AC、AB上分别取点E、F、,使得EF∥BC,把△AEF沿直线EF折起,使∠AEC=90°,得四棱锥A-ECBF(如图2).在四棱锥A-ECBF中,
已知△ABC是腰长为2的等腰直角三角形(如图1),∠BCA=90°,在边AC、AB上分别取点E、F、,使得EF∥BC,把△AEF沿直线EF折起,使∠AEC=90°,得四棱锥A-ECBF(如图2).在四棱锥A-ECBF中,查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分15分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站. 记P到三个村庄的距离之和为y.
(1)设![]() ,把y表示成
,把y表示成![]() 的函数关系式;
的函数关系式;
(2)变电站建于何处时,它到三个小区的距离之和最小?

查看答案和解析>>
科目:高中数学 来源:2013届江苏省高二上学期期末考试数学试卷(解析版) 题型:解答题
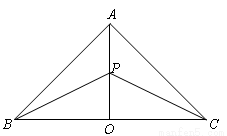
(本小题满分16分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=18km,现计划在BC边的高AO上一点P处建造一个变电站. 记P到三个村庄的距离之和为y ,(1)设 ,把y表示成
,把y表示成 的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?
的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com