
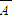 ,
,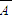 )=
)=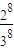 =
=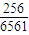 ,
,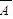 )=1-
)=1-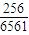 =
=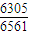 .
.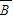 ,
,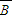 )=1-
)=1-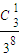 =1-
=1-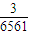 =
=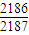 .
.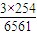 =
=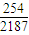 .
.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(12分)某单位一辆交通车载有4名职工从单位从发送他们下班回家,途中共有甲、乙、丙3个停车点,如果某停车点无人下车,那么该车在这个点就不停车,假设每个职工在每个停车点下车的可能性都是相等的,求
(I)该车在某停车点停车的概率
(Ⅱ)停车的次数不少于2次的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com