
【题目】实验中学在教工活动中心举办了一场台球比赛,为了节约时间比赛采取“3局2胜制”.现有甲、乙二人,已知每局甲胜的概率为0.6,乙胜的概率为0.4.求:
(1)这场比赛甲获胜的概率;
(2)这场比赛乙所胜局数的数学期望.
(3)这场比赛在甲获得比赛胜利的条件下,乙有一局获胜的概率.
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右焦点为
的左右焦点为![]() 为它的中心,
为它的中心,![]() 为双曲线右支上的一点,
为双曲线右支上的一点,![]() 的内切圆圆心为
的内切圆圆心为![]() ,且圆
,且圆![]() 与
与![]() 轴相切于
轴相切于![]() 点,过
点,过![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若双曲线的离心率为
,若双曲线的离心率为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 与
与![]() 关系不确定
关系不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非空集合![]() 是由一些函数组成,满足如下性质:①对任意
是由一些函数组成,满足如下性质:①对任意![]() ,
,![]() 均存在反函数
均存在反函数![]() ,且
,且![]() ;②对任意
;②对任意![]() ,方程
,方程![]() 均有解;③对任意
均有解;③对任意![]() 、
、![]() ,若函数
,若函数![]() 为定义在
为定义在![]() 上的一次函数,则
上的一次函数,则![]() .
.
(1)若![]() ,
,![]() ,均在集合
,均在集合![]() 中,求证:函数
中,求证:函数![]() ;
;
(2)若函数![]() (
(![]() )在集合
)在集合![]() 中,求实数
中,求实数![]() 的取值范围;
的取值范围;
(3)若集合![]() 中的函数均为定义在
中的函数均为定义在![]() 上的一次函数,求证:存在一个实数
上的一次函数,求证:存在一个实数![]() ,使得对一切
,使得对一切![]() ,均有
,均有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大湖名城,创新高地”的合肥,历史文化积淀深厚,民俗和人文景观丰富,科教资源众多,自然风光秀美,成为中小学生“研学游”的理想之地.为了将来更好地推进“研学游”项目,某旅游学校一位实习生,在某旅行社实习期间,把“研学游”项目分为科技体验游、民俗人文游、自然风光游三种类型,并在前几年该旅行社接待的全省高一学生“研学游”学校中,随机抽取了100所学校,统计如下:
研学游类型 | 科技体验游 | 民俗人文游 | 自然风光游 |
学校数 | 40 | 40 | 20 |
该实习生在明年省内有意向组织高一“研学游”学校中,随机抽取了3所学校,并以统计的频率代替学校选择研学游类型的概率(假设每所学校在选择研学游类型时仅选择其中一类,且不受其他学校选择结果的影响):
(1)若这3所学校选择的研学游类型是“科技体验游”和“自然风光游”,求这两种类型都有学校选择的概率;
(2)设这3所学校中选择“科技体验游”学校数为随机变量X,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]()
![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,椭圆的上顶点为点
,椭圆的上顶点为点![]() ,点
,点![]() 为椭圆
为椭圆![]() 上一点,且
上一点,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,求线段
两点,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间直角坐标系O-xyz中,已知正四棱锥PABCD的高OP=2,点B,D和C,A分别在x轴和y轴上,且AB=![]() ,点M是棱PC的中点.
,点M是棱PC的中点.
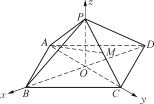
(1)求直线AM与平面PAB所成角的正弦值;
(2)求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 、
、![]() 两点分别在函数
两点分别在函数![]() 与
与![]() 的图像上,且关于直线
的图像上,且关于直线![]() 对称,则称
对称,则称![]() 、
、![]() 是
是![]() 与
与![]() 的一对“伴点”(
的一对“伴点”(![]() 、
、![]() 与
与![]() 、
、![]() 视为相同的一对).已知
视为相同的一对).已知 ,
,![]() ,若
,若![]() 与
与![]() 存在两对“伴点”,则实数
存在两对“伴点”,则实数![]() 的取值范围为________.
的取值范围为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有下列四个结论,其中所有正确结论的编号是___________.
①若![]() ,则
,则![]() 的最大值为
的最大值为![]() ;
;
②若![]() ,
,![]() ,
,![]() 是等差数列
是等差数列![]() 的前
的前![]() 项,则
项,则![]() ;
;
③“![]() ”的一个必要不充分条件是“
”的一个必要不充分条件是“![]() ”;
”;
④“![]() ,
,![]() ”的否定为“
”的否定为“![]() ,
,![]() ”.
”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com