
����Ŀ��ij�н�����ְ��겻���ĺ��飬��������Ծ��ؽ�Լ��ˮ��������ˮ���۲�ij��ˮ�ع�ˮ������ƶ���ˮ��ʩ������ij��ˮ������ˮ450�֣�ˮ��ÿСʱ������ˮ����עˮ80�֣�ͬʱ��ˮ���������С����ˮ��tСʱ�ڹ�ˮ��Ϊ![]() �֣����ڿ�ʼ��ˮ��עˮ�������С����ˮ��
�֣����ڿ�ʼ��ˮ��עˮ�������С����ˮ��
��1���뽫��ˮ���д�ˮ��S��ʾΪʱ��t�ĺ�����
��2���ʿ�ʼ��ˮ��Сʱ��ˮ�����٣�
��3������ˮ����ˮ������150��ʱ���ͻ���ֹ�ˮ������������ÿ���м�Сʱ��ˮ���ţ�
���𰸡���1��![]() ����2��
����2��![]() Сʱ����3��
Сʱ����3��![]() Сʱ.
Сʱ.
��������
��1���ɸ������⣬��ԭ�����еĴ�ˮ����ע���ˮ��ȥ��ˮ���ɵó���ˮ���д�ˮ��![]() ��ʾΪʱ��
��ʾΪʱ��![]() �ĺ�����
�����
��2����![]() ��Ȼ��ͨ����
��Ȼ��ͨ����![]() �����䷽�ó���Сֵ��
�����䷽�ó���Сֵ��
��3����![]() ���
���![]() ��ȡֵ��Χ����ͨ��
��ȡֵ��Χ����ͨ��![]() ���
���![]() ��ȡֵ��Χ�����ó������
��ȡֵ��Χ�����ó������
��1����![]() Сʱ��ˮ���д�ˮ��Ϊ
Сʱ��ˮ���д�ˮ��Ϊ![]() �֣���
�֣���![]() ��
��
��2����![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() �����Թ�ˮ
�����Թ�ˮ![]() Сʱ��ˮ����ˮ������ֻ��
Сʱ��ˮ����ˮ������ֻ��![]() �֣�
�֣�
��3����![]() �����
�����![]() ������
������![]() ������
������![]() Сʱ��ˮ���š�
Сʱ��ˮ���š�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֽ�ĸ�С���DZ߳�Ϊ1�������Σ�ͼ�д�ʵ��������һ�������������ͼ����������ͼ���������Σ���ü���������������Ϊ�� ��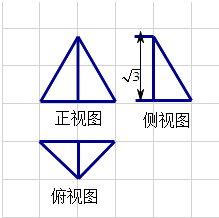
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P-ABCD�ĵ���Ϊƽ���ı��Σ�MΪPC�е㣮
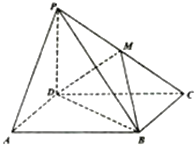
��1����֤��BA��ƽ��PCD��
��2����֤��AP��ƽ��MBD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�������Ϊ
�У�������Ϊ![]() ����Բ
����Բ![]() ����Ϊ
����Ϊ![]() ����ԭ��
����ԭ��![]() ��ֱ�ߣ���������غϣ�����Բ
��ֱ�ߣ���������غϣ�����Բ![]() ����
����![]() ���㣬ֱ��
���㣬ֱ��![]() �ֱ���
�ֱ���![]() �ύ��
�ύ��![]() ��
�� ![]() ����.��ֱ��
����.��ֱ��![]() б��Ϊ
б��Ϊ ![]() ʱ��
ʱ�� ![]() .
.
(1)����Բ![]() �ı����̣�
�ı����̣�
(2)������![]() Ϊֱ����Բ�Ƿ����㣨��ֱ��
Ϊֱ����Բ�Ƿ����㣨��ֱ��![]() ��б���أ�����֤����Ľ��ۣ�
��б���أ�����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f (x)�Ķ�������![]() ,������
,������![]()
��![]() ʱ��
ʱ��![]() �����ں���
�����ں���![]() ���������ĸ����⣺
���������ĸ����⣺
�ٺ���![]() ���溯����
���溯����
�ں���![]() �����ں�����
�����ں�����
�ۺ���![]() ��ȫ�����Ϊ
��ȫ�����Ϊ![]() ��
��
�ܵ�![]() ʱ������
ʱ������![]() ��ͼ���뺯��
��ͼ���뺯��![]() ��ͼ������ֻ�����������㣮
��ͼ������ֻ�����������㣮
����������ĸ���Ϊ ��
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
�� ![]() ����
����![]() ����
����![]() ����СֵΪ�� ��
����СֵΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
���𰸡�A
������������![]() ��
�� ![]() ����
����![]() ,��
,��![]() ��
�� ![]()
�ʴ�Ϊ��A.
�㾦�������Ŀ������Ǻ������������ı���ʽ����ֵ���������������һ�������¼��ַ�������һ������ʽ��Ӧ�ã������Ŀ�õ��Ǿ�ֵ����ʽ��ע��Ҫ����һ����������ȣ��������Ԫ��һԪ�����ٱ����ĸ�������������Ӧ�������Թ滮��֪ʶ������������Թ滮�����ں�����ʽ����Ŀ�С�
�����͡���ѡ��
��������
12
����Ŀ����֪����![]() Ϊ�Ȳ����У���
Ϊ�Ȳ����У���![]() ��������ǰ
��������ǰ![]() ���
���![]() �����ֵ����ʹ��
�����ֵ����ʹ��![]() ��
��![]() �����ֵΪ�� ��
�����ֵΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪F1 �� F2�ֱ�����Բ ![]() �����ҽ���F1 �� F2����ֱ��x+y��2=0�ĶԳƵ���ԲC��һ��ֱ���������˵㣮
�����ҽ���F1 �� F2����ֱ��x+y��2=0�ĶԳƵ���ԲC��һ��ֱ���������˵㣮
��1����ԲC�ķ��̣�
��2�������F2��ֱ��l����ԲE��ԲC���صõ��ҳ��ֱ�Ϊa��b����ab���ʱ����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ����
����![]() ��
��![]() ����ƺ���
����ƺ���![]() Ϊ��
��![]() ��������
��������
![]() ���ж�
���ж�![]() �Ƿ�Ϊ��
�Ƿ�Ϊ��![]() ����������˵�����ɣ�
����������˵�����ɣ�
![]() ����
����![]() ��
Ϊ��![]() ���������ҵ�
���������ҵ�![]() ʱ��
ʱ��![]() ����
����![]() �Ľ���ʽ����д����
�Ľ���ʽ����д����![]() �ϵĵ����������䣻
�ϵĵ����������䣻
![]() ��
��![]() �����£���
�����£���![]() ʱ������
ʱ������![]() �ķ���
�ķ���![]() Ϊ����
Ϊ����![]() �н⣬�Ǹ÷������н�ĺ�Ϊ
�н⣬�Ǹ÷������н�ĺ�Ϊ![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��= ![]() ��
��
��1����m=4ʱ������f��x���Ķ�����M��
��2����a��b��RMʱ��֤����2|a+b|��|4+ab|��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com