
已知数列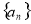 中,
中,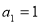 ,
, 且
且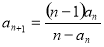
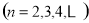 .
.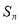 为数列
为数列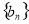 的前
的前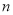 项和,且
项和,且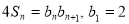
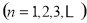 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设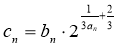 ,求数列
,求数列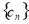 的前
的前 项的和
项的和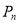 ;
;
(3)证明对一切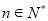 ,有
,有 .
.
(1)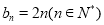 ;(2)
;(2)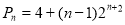 ;(3)证明过程详见解析.
;(3)证明过程详见解析.
【解析】
试题分析:本题主要考查数列的通项公式、递推公式、裂项相消法、数学归纳法、错位相减法等基础知识,考查学生分析问题解决问题的能力,转化能力和计算能力.第一问,用n-1代替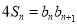 中的n,得到一个等式,2个等式相减,得到
中的n,得到一个等式,2个等式相减,得到 ,分n为奇数偶数进行讨论,分别求出
,分n为奇数偶数进行讨论,分别求出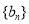 的通项公式,由于得到的式子相同,所以
的通项公式,由于得到的式子相同,所以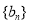 的通项公式就是
的通项公式就是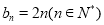 ;第二问,要求数列
;第二问,要求数列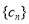 的前n项和,关键是需要求出
的前n项和,关键是需要求出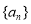 的通项公式,可以利用已知的递推公式进行推导,也可以利用数学归纳法猜想证明,得到
的通项公式,可以利用已知的递推公式进行推导,也可以利用数学归纳法猜想证明,得到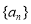 的通项公式后,代入到
的通项公式后,代入到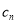 中,得到
中,得到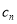 的通项公式,最后用错位相减法进行求和;第三问,先用放缩法对原式进行变形,再用裂项相消法求和,最后和
的通项公式,最后用错位相减法进行求和;第三问,先用放缩法对原式进行变形,再用裂项相消法求和,最后和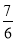 作比较.
作比较.
试题解析:(1)由已知 得
得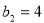 ,
,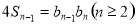 ,
,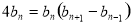 ,
,
由题意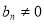 ,即
,即 ,当n为奇数时,
,当n为奇数时,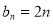 ;当n为偶数时,
;当n为偶数时,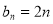 .
.
所以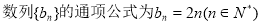 .4分
.4分
(2)解法一:由已知,对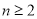 有
有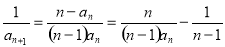 ,
,
两边同除以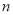 ,得
,得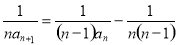 ,即
,即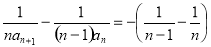 ,
,
于是, =
=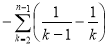 =
=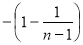 ,
,
即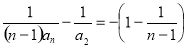 ,
,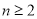 ,所以
,所以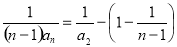 =
=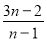 ,
,
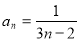 ,
,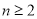 ,又
,又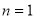 时也成立,故
时也成立,故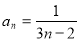 ,
,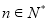 .
.
所以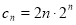 ,
,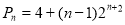 8分
8分
解法二:也可以归纳、猜想得出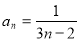 ,然后用数学归纳法证明.
,然后用数学归纳法证明.
(3)当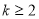 ,有
,有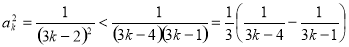 ,
,
所以 时,有
时,有
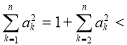
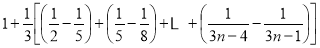
=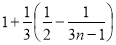
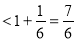 .
.
当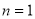 时,
时,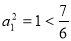 .故对一切
.故对一切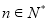 ,有
,有 .14分
.14分
考点:1.由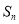 求
求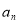 ;2.错位相减法;3.数学归纳法;4.裂项相消法.
;2.错位相减法;3.数学归纳法;4.裂项相消法.


 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二理科数学试卷(解析版) 题型:选择题
一个几何体的三视图如图,则该几何体的体积为( )
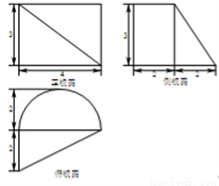
A.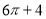 B.
B.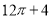 C.
C.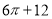 D.
D.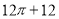
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
对任意实数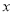 、
、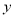 ,定义运算
,定义运算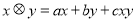 ,其中
,其中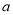 、
、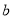 、
、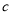 是常数,等式右边的运算
是常数,等式右边的运算
是通常的加法和乘法运算.已知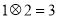 ,
,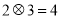 ,并且有一个非零常数
,并且有一个非零常数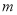 ,使得
,使得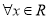 ,都有
,都有
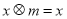 ,则
,则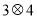 的值是( )
的值是( )
A.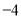 B.
B.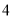 C.
C.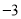 D.
D.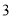
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
如图是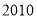 年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为( )
年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为( )
A.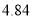 B.
B.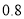 C.
C.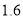 D.
D.
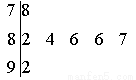
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)理科数学试卷(解析版) 题型:填空题
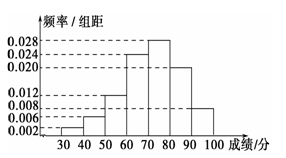
某中学为了解学生数学课程的学习情况,在3 000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3 000名学生在该次数学考试中成绩小于60分的学生数是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)文科数学试卷(解析版) 题型:填空题
如图,有一个形如六边形的点阵,它的中心是一个点(算第1层),第2层每边有两个点,第3层每边有三个点,依次类推.
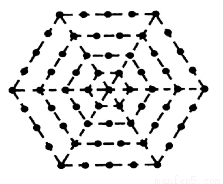
(1)试问第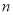 层
层 的点数为___________个;
的点数为___________个;
(2)如果一个六边形点阵共有169个点,那么它一共有_____层.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com