练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】定义：若函数的图像经过变换后所得的图像对应的函数与的值域相同，则称变换是的同值变换，下面给出了四个函数与对应的变换：

    ①将函数的图像关于轴作对称变换；

    ②将函数的图像关于轴作对称变换；

    ③将函数的图像关于点（-1，1）作对称变换；

    ④将函数的图像关于点（-1，0）作对称变换；

    其中是的同值变换的有_______.（写出所有符合题意的序号）

    【答案】①③④

    【解析】

    根据同值变换的定义对四个变换逐一分析，由此确定是的同值变换.

    对于①，关于轴对称变换时，值域保持不变，故①符合.

    对于②，由于，即值域为，关于轴对称变换后的值域为，故②不符合.

    对于③，，所以图像关于对称，故③符合.

    对于④的值域为，关于对称后为，故④符合.

    故答案为：①③④.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四边形中，，，四边形为矩形，且平面，.

    （1）求证：平面；

    （2）点在线段上运动，当点在什么位置时，平面与平面所成锐二面角最大，并求此时二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校象棋社团组织中国象棋比赛,采用单循环赛制,即要求每个参赛选手必须且只须和其他选手各比赛一场,胜者得分,负者得分,平局两人各得分.若冠军获得者得分比其他人都多,且获胜场次比其他人都少,则本次比赛的参赛人数至少为

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中.

    （1）令，判断函数的奇偶性，并说明理由；

    （2）令，的最大值为A，函数在区间上单调递增函数，求的取值范围；

    （3）令，将函数的图像向左平移个单位，再向上平移1个单位，得到函数的图像，对任意，求在区间上零点个数的所有可能值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若存在常数，使得数列满足对一切恒成立，则称为可控数列，.

    （1）若，，问有多少种可能？

    （2）若是递增数列，，且对任意的，数列，，成等差数列，判断是否为可控数列？说明理由；

    （3）设单调的可控数列的首项，前项和为，即.问的极限是否存在，若存在，求出与的关系式；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知各项均为正数的数列的前项和为且满足:

    (1)求数列的通项公式；

    (2)设求的值；

    (3)是否存在大于2的正整数使得?若存在,求出所有符合条件的若不存在,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    (1)若是函数的一个极值点，试求的单调区间；

    (2)若且，是否存在实数a，使得在区间上的最大值为4?若存在，求出实数a的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，两铁路线垂直相交于站，若已知千米，甲火车从站出发，沿方向以千米小时的速度行驶，同时乙火车从站出发，沿方向，以千米小时的速度行驶，至站即停止前行（甲车扔继续行驶）（两车的车长忽略不计）.

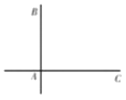
    （1）求甲、乙两车的最近距离（用含的式子表示）；

    （2）若甲、乙两车开始行驶到甲，乙两车相距最近时所用时间为小时，问为何值时最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，其中.

    （1）若，写出的单调区间：

    （2）若函数恰有三个不同的零点，且这些零点之和为-2，求a、b的值；

    （3）若函数在上有四个不同零点，求的最大值。

    查看答案和解析>>

    同步练习册答案