
分析 根据题意可得,[log21]=0有1个0,[log22]=[log23]=1,有2个1,[log24]=[log25]=…=[log27]=2,有4个2,[log28]=[log29]=[log210]=…=[log215]=3,有8个3,[log2512]=9,则[log21]+[log22]+[log23]+[log24]+…+[log21024]=1×2+2×22+3×23+…+8×28+9,令S=1×2+2×22+…+8×28,利用错位相减可求S,进而可求.
解答 解:根据题意可得,[log21]=0有1个0,[log22]=[log23]=1,有2个1,[log24]=[log25]=…=[log27]=2,有4个2
[log28]=[log29]=[log210]=…=[log215]=3,有8个3,[log21024]=10
所以,[log21]+[log22]+[log23]+[log24]+…+[log2512]
=0+1+1+2+2+2+2+3+3+3+3+3+3+3+3+…+9
=1×2+2×22+3×23+…+8×28+9
令S=1×2+2×22+…+8×28
2S=1×22+2×23+…+8×29
所以,-S=2+22+…+28-8×29
=$\frac{2(1-{2}^{8})}{1-2}$-8×29=-2-7×29
S=7×29+2=3586.
∴[log21]+[log22]+[log23]+[log24]+…+[log2512]=S+9=3586+9=3595.
故答案为:3595.
点评 本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意对数性质和错位相减法的合理运用.


科目:高中数学 来源: 题型:解答题
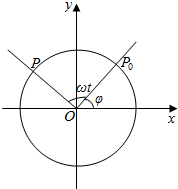 如图,点P是半径为rcm的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针以角速度ωrαd/s做圆周运动,求点P的纵坐标y关于时间t的函数关系,并求点P的运动周期和频率.
如图,点P是半径为rcm的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针以角速度ωrαd/s做圆周运动,求点P的纵坐标y关于时间t的函数关系,并求点P的运动周期和频率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com