
【题目】在杨辉三角形中,从第2行开始,除1以外,其它每一个数值是它上面的两个数值之和,该三角形数阵开头几行如图所示.

(1)在杨辉三角形中是否存在某一行,使该行中三个相邻的数之比是3∶4∶5?若存在,试求出是第几行;若不存在,请说明理由;
(2)已知n,r为正整数,且n≥r+3.求证:任何四个相邻的组合数C,C![]() ,C
,C![]() ,C
,C![]() 不能构成等差数列.
不能构成等差数列.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1) 杨辉三角形的第![]() 行由二项式系数
行由二项式系数![]() 组成.
组成.
若第![]() 行中有三个相邻的数之比为
行中有三个相邻的数之比为![]() 则
则 ![]()
解之即可说明存在;
利用组合数公式可得![]() 两式相减得
两式相减得![]() ,所以C
,所以C![]() ,C
,C![]() ,C
,C![]() ,C
,C![]() 成等差数列,由二项式系数的性质可知C
成等差数列,由二项式系数的性质可知C![]() =C
=C![]() <C
<C![]() =C
=C![]() ,这与等差数列的性质矛盾,从而要证明的结论成立
,这与等差数列的性质矛盾,从而要证明的结论成立
试题解析:(1)解 存在.杨辉三角形的第n行由二项式系数C,k=0,1,2,…,n组成.
若第n行中有三个相邻的数之比为3∶4∶5,
则![]() ,
,
即3n-7k=-3,4n-9k=5,解得k=27,n=62.
即第62行有三个相邻的数C![]() ,C
,C![]() ,C
,C![]() 的比为3∶4∶5.
的比为3∶4∶5.
(2)证明 若有n,r(n≥r+3),使得C,C![]() ,C
,C![]() ,C
,C![]() 成等差数列,
成等差数列,
则2C![]() =C+C
=C+C![]() ,2C
,2C![]() =C
=C![]() +C
+C![]() ,
,
即![]() =
=![]() +
+![]() ,
,
![]()
=![]() +
+![]() ,
,
所以![]() =
=![]() +
+![]() ,
,
![]() =
=![]() +
+![]() ,
,
整理得n2-(4r+5)n+4r(r+2)+2=0,n2-(4r+9)n+4(r+1)(r+3)+2=0.
两式相减得n=2r+3,
所以C![]() ,C
,C![]() ,C
,C![]() ,C
,C![]() 成等差数列,
成等差数列,
由二项式系数的性质可知C![]() =C
=C![]() <C
<C![]() =C
=C![]() ,
,
这与等差数列的性质矛盾,从而要证明的结论成立


科目:高中数学 来源: 题型:
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足:①a1=1;②所有项an∈N*;③1=a1<a2<…<an<an+1<….设集合Am={n|an≤m,m∈N*),将集合Am中的元素的最大值记为bm,即bm是数列{an}中满足不等式an≤m的所有项的项数的最大值.我们称数列{bn}为数列{an}的伴随数列.
例如,数列1,3,5的伴随数列为1,1,2,2,3.
(I)若数列{an}的伴随数列为1,1,2,2,2,3,3,3,3……,请写出数列{an};
(II)设an=4n-1,求数列{an}的伴随数列{bn}的前50项之和;
(III)若数列{an}的前n项和![]() (其中c为常数),求数列{an}的伴随数列{bm}的前m项和Tm.
(其中c为常数),求数列{an}的伴随数列{bm}的前m项和Tm.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(一)在函数图象的学习中常常用到化归转化的思想,往往通过对一些已经学习过的函数图象的研究,进一步迁移到其它函数,例如函数![]() 与正弦函数就有密切的联系,因为
与正弦函数就有密切的联系,因为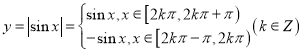 .只需将
.只需将![]() 在
在![]() 轴下方的图象翻折到上方,就得到
轴下方的图象翻折到上方,就得到![]() 的图象.
的图象.
(二)在研究函数零点问题时,往往会将函数零点问题转化为两个函数图象的交点问题.例如研究函数![]() 的零点就可以转化为函数
的零点就可以转化为函数![]() 与函数
与函数![]() 的图象交点来进行处理,通过作图不仅知道函数
的图象交点来进行处理,通过作图不仅知道函数![]() 有且仅有一个零点,还可以确定零点
有且仅有一个零点,还可以确定零点![]() .这体现了化归转化与数形结合的思想在函数研究中的应用.
.这体现了化归转化与数形结合的思想在函数研究中的应用.
结合阅读材料回答下面两个问题:
![]() 作出函数
作出函数![]() 的图象;
的图象;
![]() 利用作图的方法验证函数
利用作图的方法验证函数![]() 有且仅有两个零点.若记两个零点分别为
有且仅有两个零点.若记两个零点分别为![]() ,
,![]() ,证明:
,证明:![]() .(注:在同一坐标中作图)
.(注:在同一坐标中作图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com