已知函数f(x)=ax2+bx-1(a,b为实数),x∈R,
(1)若不等式f(x)>2的解集为{x|x<-3或x>1},求f(x)在区间[-2,3)的值域;
(2)在(1)的条件下,当x∈[-1,1]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
解:(1)由题意可得不等式f(x)>2的解集为{x|x<-3或x>1},
即不等式ax
2+bx-3>0的解集为{x|x<-3或x>1},
∴-3和1是方程ax
2+bx-3=0的两根,∴

解得
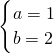
,∴f(x)=x
2+2x-1=(x+1)
2-2
∴x∈[-2,3)时,f(x)
min=f(-1)=-2,f(x)<f(3)=14
∴求f(x)在区间[-2,3)的值域为:[-2,14)
(2)由(1)知,g(x)=x
2+2x-1-kx=x
2+(2-k)x-1
∴g(x)的图象为开口向上的抛物线,对称轴为x=
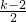
若函数g(x)[-1,1]上是单调函数,则
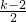
≤-1或
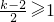
,解得k≤0,或k≥4
故实数k的取值范围为k≤0,或k≥4
分析:(1)由题意可得ax
2+bx-3>0的解集为{x|x<-3或x>1},即-3和1是方程ax
2+bx-3=0的两根,可解ab的值,通过二次函数区间的最值可解;
(2)由(1)知,g(x)=x
2+2x-1-kx=x
2+(2-k)x-1,其图象为开口向上的抛物线,对称轴为x=
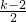
,题意可化为
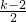
≤-1或
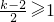
,解之即可.
点评:本题为不等式的解集与二次函数的结合,涉及函数的单调性,属基础题.


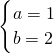 ,∴f(x)=x2+2x-1=(x+1)2-2
,∴f(x)=x2+2x-1=(x+1)2-2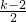
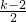 ≤-1或
≤-1或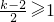 ,解得k≤0,或k≥4
,解得k≤0,或k≥4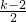 ,题意可化为
,题意可化为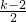 ≤-1或
≤-1或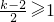 ,解之即可.
,解之即可.
