练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某校有、、、四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖，在结果揭晓前，甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.

    甲说：“、同时获奖.”

    乙说：“、不可能同时获奖.”

    丙说：“获奖.”

    丁说：“、至少一件获奖”

    如果以上四位同学中有且只有两位同学的预测是正确的，则获奖的作品是（ ）

    A. 作品与作品B. 作品与作品C. 作品与作品D. 作品与作品

    【答案】D

    【解析】

    根据条件可判断出乙丁预测正确，而甲丙预测错误，这样根据这四位同学的预测即可得出获奖的作品．

    乙，丁预测的是正确的，甲，丙预测的是错误的；

    丙预测错误，∴C不获奖；

    丁预测正确，A，C至少一件获奖，∴A获奖；

    甲预测错误，即A，B不同时获奖，∴B不获奖；

    ∴D获奖；

    即获奖的作品是作品A与作品D．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在数列中，、是给定的非零整数，．

    （1）若，，求；

    （2）证明：从中一定可以选取无穷多项组成两个不同的常数项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

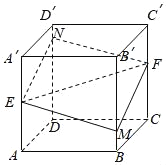
    【题目】如图所示，正方体ABCD﹣A′B′C′D′的棱长为1，E，F分别是棱AA′，CC′的中点，过直线E，F的平面分别与棱BB′、DD′交于M，N，设BM＝x，x∈[0，1]，给出以下四个命题：

    ①平面MENF⊥平面BDD′B′；

    ②当且仅当x＝时，四边形MENF的面积最小；

    ③四边形MENF周长L＝f（x），x∈[0，1]是单调函数；

    ④四棱锥C′﹣MENF的体积V＝h（x）为常函数；

    以上命题中假命题的序号为（　　）

    A. ①④B. ②C. ③D. ③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表：

    温度x/C

    21

    23

    24

    27

    29

    32

    产卵数y/个

    6

    11

    20

    27

    57

    77

    经计算得： ， ， ， ，

    ，线性回归模型的残差平方和，e8.0605≈3167，其中xi, yi分别为观测数据中的温度和产卵数，i=1, 2, 3, 4, 5, 6.

    (Ⅰ)若用线性回归模型，求y关于x的回归方程=x+（精确到0.1）；

    (Ⅱ)若用非线性回归模型求得y关于x的回归方程为=0.06e0.2303x，且相关指数R2=0.9522.

    ( i )试与(Ⅰ)中的回归模型相比，用R2说明哪种模型的拟合效果更好.

    ( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数（结果取整数）.

    附：一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线=x+的斜率和截距的最小二乘估计为

    =；相关指数R2=．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求在上的最值；

    （2）若，当有两个极值点时，总有，求此时实数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设集合A={（x，y）|（x-4）2+y2=1}，B={（x，y）|（x-t）2+（y-at+2）2=1}，如果命题“t∈R，A∩B≠”是真命题，则实数a的取值范围是（　　）

    A.B.

    C.D.,

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点， 轴为极轴建立极坐标系，曲线的极坐标为．

    （1）求曲线的普通方程和曲线的直角坐标方程；

    （2）若曲线和曲线有三个公共点，求以这三个公共点为顶点的三角形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （Ⅰ）当时，求函数的单调区间；

    （Ⅱ）若在区间上存在不相等的实数,使成立，求的取值范围；

    （Ⅲ）若函数有两个不同的极值点，，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】朱世杰是历史上最伟大的数学家之一，他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题：今有官司差夫一千八百六十四人筑堤，只云初日差六十四人，次日转多七人.”其大意为“官府陆续派遣1864人前往修筑堤坝，第一天派出64人，从第二天开始每天派出的人数比前一天多7人.”在该问题中的1864人全部派遣到位需要的天数为（ ）

    A. 9B. 16C. 18D. 20

    查看答案和解析>>

    同步练习册答案