
【题目】在![]() 中,设边
中,设边![]() ,
,![]() ,
,![]() 所对的角分别为
所对的角分别为![]() ,
,![]() ,
,![]() ,已知
,已知![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用正弦定理可将原式化简为cosA![]() sinA
sinA![]() ,整理得
,整理得![]() sinC﹣cosC=1,即sin(C
sinC﹣cosC=1,即sin(C![]() )
)![]() ,进而可得C的大小;
,进而可得C的大小;
(2)利用余弦定理可将cosB![]() 化成
化成![]() ,即8sinAcosB=5sinC=5sin
,即8sinAcosB=5sinC=5sin![]() ,进而求出sinAcosB的值.
,进而求出sinAcosB的值.
(1)△ABC中,![]() ,即cosA
,即cosA![]() sinA
sinA![]() ,
,
∴sinCcosA![]() sinAsinC=sinB+sinA,
sinAsinC=sinB+sinA,
∵sinB+sinA=sin(A+C)+sinA=sinAcosC+sinCcosA+sinA,
∴sinCcosA![]() sinAsinC=sinAcosC+sinCcosA+sinA,可得
sinAsinC=sinAcosC+sinCcosA+sinA,可得![]() sinAsinC=sinAcosC+sinA,
sinAsinC=sinAcosC+sinA,
∵sinA≠0,
∴![]() sinC﹣cosC=1,即sin(C
sinC﹣cosC=1,即sin(C![]() )
)![]() ,
,
∵C∈(0,π),C![]() ∈(
∈(![]() ,
,![]() ),
),
∴C![]() ,可得C
,可得C![]() .
.
(2)若![]() ,则cosB
,则cosB![]() ,即8sinAcosB=5sinC=5sin
,即8sinAcosB=5sinC=5sin![]() ,
,
所以sinAcosB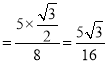 .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,动点
中,动点![]() (其中
(其中![]() )到点
)到点![]() 的距离的
的距离的![]() 倍与点
倍与点![]() 到直线
到直线![]() 的距离的
的距离的![]() 倍之和记为
倍之和记为![]() ,且
,且![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)=a![]() (a为常数).
(a为常数).
(1)求a的值;
(2)若函数g(x)=|(2x+1)f(x)|﹣k有2个零点,求实数k的取值范围;
(3)若x∈[﹣2,﹣1]时,不等式f(x)![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的离心率正好是双曲线
的离心率正好是双曲线![]() 的离心率的倒数,椭圆
的离心率的倒数,椭圆![]() 的短轴长等于抛物线
的短轴长等于抛物线![]() 上一点
上一点![]() 到抛物线焦点
到抛物线焦点![]() 的距离.
的距离.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 的两个交点为
的两个交点为![]() ,
,![]() 两点,已知圆
两点,已知圆![]() :
:![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() (点
(点![]() 在
在![]() 轴的正半轴),且直线
轴的正半轴),且直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的面积与
的面积与![]() 的面积乘积的最大值.
的面积乘积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com