
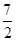 ,|AF2|=
,|AF2|=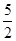 .
.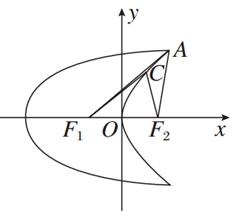
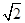 |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.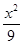 +
+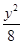 =1(-3≤x≤
=1(-3≤x≤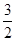 ),曲线C2的方程为y2=4x(0≤x≤
),曲线C2的方程为y2=4x(0≤x≤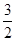 )
)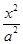 +
+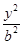 =1(a>b>0),则2a=|AF1|+|AF2|=
=1(a>b>0),则2a=|AF1|+|AF2|=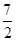 +
+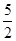 =6,得a=3.
=6,得a=3.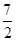 )2,(x-c)2+y2=(
)2,(x-c)2+y2=(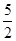 )2,两式相减得xc=
)2,两式相减得xc=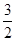 .由抛物线的定义可知|AF2|=x+c=
.由抛物线的定义可知|AF2|=x+c=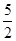 ,
,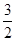 或x=1,c=
或x=1,c=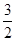 .又∠AF2F1为钝角,
.又∠AF2F1为钝角,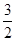 不合题意,舍去.当c=1时,b=2
不合题意,舍去.当c=1时,b=2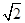 ,
,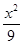 +
+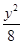 =1(-3≤x≤
=1(-3≤x≤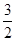 ),曲线C2的方程为y2=4x(0≤x≤
),曲线C2的方程为y2=4x(0≤x≤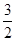 ).
).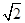 |CF2|=
|CF2|=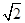 |CC1|,所以∠C1CF1=45°,
|CC1|,所以∠C1CF1=45°,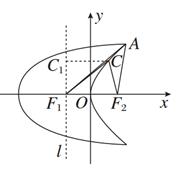
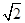 r,|F1F2|=2.
r,|F1F2|=2.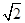 r)2-2×2×
r)2-2×2×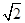 rcos45°=r2,
rcos45°=r2,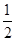 |F1F2|·|CF1|sin45°=
|F1F2|·|CF1|sin45°=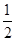 ×2×2
×2×2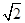 sin45°=2.
sin45°=2.

 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源:不详 题型:解答题
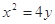 ,过点
,过点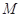
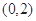 作直线与抛物线交于两点
作直线与抛物线交于两点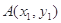 ,
,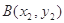 ,过
,过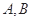 分别作抛物线的切线,两切线的交点为
分别作抛物线的切线,两切线的交点为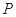 .
.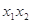 的值;
的值;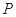 的纵坐标;
的纵坐标;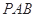 面积的最小值.
面积的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
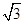 ,且其三个顶点均在抛物线E:x2=2py(p>0)上.
,且其三个顶点均在抛物线E:x2=2py(p>0)上.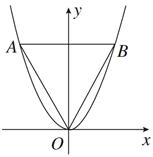
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com