练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】现安排6名同学前往4所学校进行演讲，要求甲、乙两同学不能前往同一个学校，每个学校都有人前往，每人只前往一个学校，则满足上述要求的不同安排方案数为________．（用数字作答）

    【答案】1320

    【解析】

    分4所学校人数是3，1，1，1和2，2，1，1两种情况讨论，采用间接法来处理.

    安排6名同学前往4所学校进行演讲，每个学校都有人前往，每人只前往一个学校，有两种情况：

    若4所学校的人数是3，1，1，1时，则有种不同安排方式，当甲、乙前往同一学校时，

    有种不同的安排方式；

    若4所学校的人数是2，2，1，1时，则有种不同安排方式，当甲、乙前往同一学校时，

    有种不同的安排方式；

    故甲、乙两同学不能前往同一个学校，每个学校都有人前往，每人只前往一个学校共有

    种.

    故答案为：1320

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知点是椭圆的左、右焦点，点是该椭圆上一点，若当时，面积达到最大，最大值为.

    （1）求椭圆的标准方程；

    （2）设为坐标原点，是否存在过左焦点的直线，与椭圆交于两点，使得的面积为？若存在，求出直线的方程；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某少儿游泳队需对队员进行限时的仰卧起坐达标测试.已知队员的测试分数与仰卧起坐

    个数之间的关系如下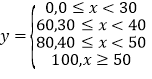：；测试规则：每位队员最多进行三组测试，每组限时1分钟，当一组测完，测试成绩达到60分或以上时，就以此组测试成绩作为该队员的成绩，无需再进行后续的测试，最多进行三组；根据以往的训练统计，队员“喵儿”在一分钟内限时测试的频率分布直方图如下：

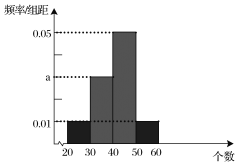
    （1）计算值；

    （2）以此样本的频率作为概率，求

    ①在本次达标测试中，“喵儿”得分等于的概率；

    ②“喵儿”在本次达标测试中可能得分的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下面类比推理：

    ①“若2a<2b，则a<b”类比推出“若a2<b2，则a<b”；

    ②“(a＋b)c＝ac＋bc(c≠0)”类比推出“ (c≠0)”；

    ③“a，b∈R，若a－b＝0，则a＝b”类比推出“a，b∈C，若a－b＝0，则a＝b”；

    ④“a，b∈R，若a－b>0，则a>b”类比推出“a，b∈C，若a－b>0，则a>b(C为复数集)”．

    其中结论正确的个数为(　　)

    A. 1B. 2C. 3D. 4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    (Ⅰ)当时，讨论函数的单调区间；

    (Ⅱ)若对任意的和恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，设抛物线的焦点为F，点P是半椭圆上的一点，过点P作抛物线C的两条切线，切点分别为A、B，且直线PA、PB分别交y轴于点M、N．

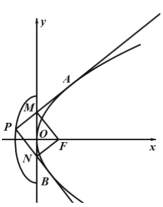
    （1）证明：；

    （2）求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面平面，，，.

    （1）证明：；

    （2）设点M在线段PC上，且，若的面积为，求四棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C的顶点在坐标原点，焦点在坐标轴上.

    （1）若抛物线C经过点，求C的标准方程；

    （2）抛物线C的焦点（m是大于零的常数），若过点F的直线与C交于 两点，，求面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知,命题:对,不等式恒成立;命题,使得成立.

    (1)若为真命题,求的取值范围;

    (2)当时,若假,为真,求的取值范围.

    查看答案和解析>>

    同步练习册答案