
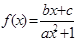 (
(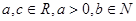 )是奇函数,
)是奇函数,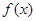 有最大值
有最大值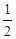
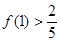 .
.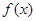 的解析式;
的解析式;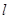 与
与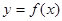 的图象交于P、Q两点,并且使得
的图象交于P、Q两点,并且使得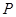 、
、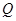 两点关于点
两点关于点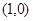 对称,若存在,求出直线
对称,若存在,求出直线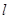 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.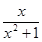 (2)过P、Q的直线l的方程:x-4y-1=0
(2)过P、Q的直线l的方程:x-4y-1=0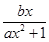 .由a>0,
.由a>0,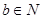 ,所以当x>0时,才可能取得最大值,所以x>0时,
,所以当x>0时,才可能取得最大值,所以x>0时,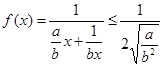 当且仅当
当且仅当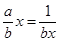 ,即
,即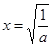 时,f(x)有最大值
时,f(x)有最大值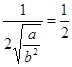 ,
,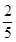 ,∴
,∴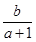 >
>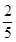 ,
,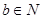 ,可求出a,b的值.
,可求出a,b的值. ,
,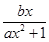 .由a>0,
.由a>0,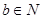 , 当x≤0时,f(x)≤0,
, 当x≤0时,f(x)≤0,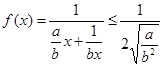 当且仅当
当且仅当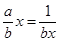
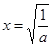 时,f(x)有最大值
时,f(x)有最大值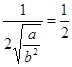 ∴
∴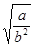 =1,∴a=b2 ①
=1,∴a=b2 ①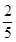 ,∴
,∴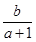 >
>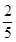 ,∴5b>2a+2 ②
,∴5b>2a+2 ②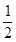 <b<2,又b∈N,∴b="1,a=1," ----------4分
<b<2,又b∈N,∴b="1,a=1," ----------4分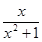 ------------7分
------------7分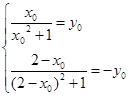 ,消去y0,得x02–2x0–1=0---9分
,消去y0,得x02–2x0–1=0---9分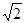 ,∴P点坐标为(
,∴P点坐标为(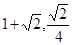 )或(
)或(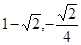 ),
),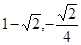 )或Q(
)或Q(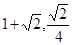 ), -------11分
), -------11分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
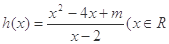 ,且
,且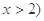 ,函数
,函数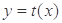 的图象经过点
的图象经过点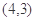 ,且
,且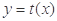 与
与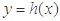 的图象关于直线
的图象关于直线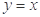 对称,将函数
对称,将函数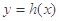 的图象向左平移2个单位后得到函数
的图象向左平移2个单位后得到函数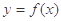 的图象.
的图象.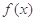 的解析式;
的解析式;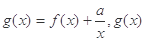 在区间
在区间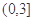 上的值不小于8,求实数
上的值不小于8,求实数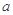 的取值范围.
的取值范围.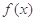 满足:对任意的
满足:对任意的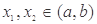 (其中
(其中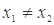 ),有
),有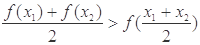 ,称函数
,称函数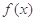 在
在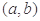 的图象是“下凸的”.判断此题中的函数
的图象是“下凸的”.判断此题中的函数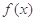 图象在
图象在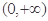 是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
是否是“下凸的”?如果是,给出证明;如果不是,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com