
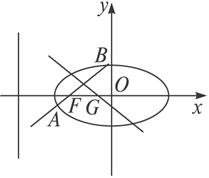
(1)求过点O、F,并且与椭圆的左准线l相切的圆的方程;
(2)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
解:(1)∵a2=2,b2=1,
∴c=1,F(-1,0),l:x=-2
∵圆过点O、F,
∴圆心M在直线x=![]() 上.
上.
设M(![]() ,t),则圆半径
,t),则圆半径
r=|(![]() )-(-2)|=
)-(-2)|=![]() .
.
由|OM|=r,得![]() ,
,
解得t=±![]() .
.
∴所求圆的方程为(x+![]() )2+(y±
)2+(y±![]() )2=
)2=![]() .
.
(2)设直线AB的方程为y=k(x+1)(k≠0),
代入![]() +y2=1,整理得(1+2k2)x2+4k2x+2k2-2=0.
+y2=1,整理得(1+2k2)x2+4k2x+2k2-2=0.
∵直线AB过椭圆的左焦点F,
∴方程有两个不等实根.
记A(x1,y1),B(x2,y2),AB中点N(x0,y0),
则x1+x2=![]() ,
,
∴AB的垂直平分线NG的方程为y-y0=![]() (x-x0).
(x-x0).
令y=0,得xG=x0+ky0=![]() .
.
∵k≠0,∴-12<xG<0,
∴点G横坐标的取值范围为(![]() ,0).
,0).


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:

(1)设直线AB与直线OM的斜率分别为k1、k2,且k1·k2=![]() ,求椭圆的离心率;
,求椭圆的离心率;
(2)若直线AB经过椭圆的右焦点F,且四边形OACB是平行四边形,求直线AB斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省莆田市仙游一中、六中高二(上)期末数学试卷(理科)(解析版) 题型:解答题
 +y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.
+y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.查看答案和解析>>
科目:高中数学 来源:2010年江西省名校高考数学信息卷1(理科)(解析版) 题型:选择题
 +y2=1上一点M到点(1,0)的距离是
+y2=1上一点M到点(1,0)的距离是 ,则点M到直线x=-2的距离是( )
,则点M到直线x=-2的距离是( )
查看答案和解析>>
科目:高中数学 来源:2010年东北三省长春、哈尔滨、沈阳、大连第二次联考数学试卷(理科)(解析版) 题型:选择题
 +y2=1(a>1)的两个焦点为F1、F2,P为椭圆上一点,且∠F1PF2=60°,则|PF1|•|PF2|的值为( )
+y2=1(a>1)的两个焦点为F1、F2,P为椭圆上一点,且∠F1PF2=60°,则|PF1|•|PF2|的值为( )


查看答案和解析>>
科目:高中数学 来源:2010年吉林省长春市高考数学三模试卷(理科)(解析版) 题型:选择题
 +y2=1(a>1)的两个焦点为F1、F2,P为椭圆上一点,且∠F1PF2=60°,则|PF1|•|PF2|的值为( )
+y2=1(a>1)的两个焦点为F1、F2,P为椭圆上一点,且∠F1PF2=60°,则|PF1|•|PF2|的值为( )


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com