练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某单位准备购买三台设备，型号分别为已知这三台设备均使用同一种易耗品，提供设备的商家规定：可以在购买设备的同时购买该易耗品，每件易耗品的价格为100元，也可以在设备使用过程中，随时单独购买易耗品，每件易耗品的价格为200元.为了决策在购买设备时应购买的易耗品的件数.该单位调查了这三种型号的设备各60台，调査每台设备在一个月中使用的易耗品的件数，并得到统计表如下所示.

    每台设备一个月中使用的易耗品的件数

    6

    7

    8

    型号A

    30

    30

    0

    频数

    型号B

    20

    30

    10

    型号C

    0

    45

    15

    将调查的每种型号的设备的频率视为概率，各台设备在易耗品的使用上相互独立.

    （1）求该单位一个月中三台设备使用的易耗品总数超过21件的概率；

    （2）以该单位一个月购买易耗品所需总费用的期望值为决策依据，该单位在购买设备时应同时购买20件还是21件易耗品？

    【答案】（1）（2）应该购买21件易耗品

    【解析】

    （1）由统计表中数据可得型号分别为在一个月使用易耗品的件数为6,7,8时的概率,设该单位三台设备一个月中使用易耗品的件数总数为X,则,利用独立事件概率公式进而求解即可；

    （2）由题可得X所有可能的取值为,即可求得对应的概率,再分别讨论该单位在购买设备时应同时购买20件易耗品和21件易耗品时总费用的可能取值及期望,即可分析求解.

    （1）由题中的表格可知

    A型号的设备一个月使用易耗品的件数为6和7的频率均为；

    B型号的设备一个月使用易耗品的件数为6,7,8的频率分别为；

    C型号的设备一个月使用易耗品的件数为7和8的频率分别为；

    设该单位一个月中三台设备使用易耗品的件数分别为,则

    ,,,

    设该单位三台设备一个月中使用易耗品的件数总数为X,

    则

    而

    ,

    ,

    故,

    即该单位一个月中三台设备使用的易耗品总数超过21件的概率为.

    （2）以题意知,X所有可能的取值为

    ；

    ；

    ；

    由（1）知,,

    若该单位在购买设备的同时购买了20件易耗品,设该单位一个月中购买易耗品所需的总费用为元,则的所有可能取值为,

    ；

    ；

    ；

    ；

    ；

    若该单位在肋买设备的同时购买了21件易耗品,设该单位一个月中购买易耗品所需的总费用为元,则的所有可能取值为,

    ；

    ；

    ；

    ；

    ,所以该单位在购买设备时应该购买21件易耗品

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求函数的单调区间；

    （2）当时，若，恒成立，求实数的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某超市销售某种商品，据统计，该该商品每日的销售量（单位：千克）与销售价格（单位：元/千克，其中）满足：当时，（，为常数）；当时，，已知当销售价格为6元/千克时，每日售出该商品170千克.

    （1）求，的值，并确定关于的函数解析式；

    （2）若该商品的销售成本为3元/千克，试确定销售价格的值，使店铺每日销售该商品所获利润最大.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来，南宁大力实施“二产补短板、三产强优势、一产显特色”策略，着力发展实体经济，工业取得突飞猛进的发展.逐步形成了以电子信息、机械装备、食品制糖、铝深加工等为主的4大支柱产业.广西洋浦南华糖业积极响应号召，大力研发新产品，为了对新研发的一批产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组销售数据，如下表所示，已知.

    （1）求出q的值；

    （2）已知变量x，y具有线性相关关系，求产品销量y(件)关于试销单价x(元)的线性回归方程；

    （3）用表示用（2）中所求的线性回归方程得到的与对应的产品销量的估计值.当销售数据对应的残差的绝对值时，则将销售数据称为一个“好数据”.现从6个销售数据中任取3个，求“好数据”个数的数学期望Eξ.

    (参考公式：线性回归方程中的最小二乘估计分别为：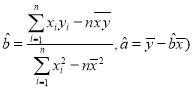

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知的展开式中第5项与第7项的二项数系数相等，且展开式的各项系数之和为1024，则下列说法正确的是（ ）

    A.展开式中奇数项的二项式系数和为256

    B.展开式中第6项的系数最大

    C.展开式中存在常数项

    D.展开式中含项的系数为45

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂采用甲、乙两种不同生产方式生产某零件，现对两种生产方式所生产的这种零件的产品质量进行对比，其质量按测试指标可划分为：指标在区间100的为一等品；指标在区间的为二等品现分别从甲、乙两种不同生产方式所生产的零件中，各自随机抽取100件作为样本进行检测，测试指标结果的频率分布直方图如图所示：

    若在甲种生产方式生产的这100件零件中按等级，利用分层抽样的方法抽取10件，再从这10件零件中随机抽取3件，求至少有1件一等品的概率；

    将频率分布直方图中的频率视作概率，用样本估计总体若从该厂采用乙种生产方式所生产的所有这种零件中随机抽取3件，记3件零件中所含一等品的件数为X，求X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来，我国许多省市雾霾天气频发，为增强市民的环境保护意识，某市面向全市征召名义务宣传志愿者，成立环境保护宣传组织，现把该组织的成员按年龄分成组第组，第组，第组，第组，第组，得到的频率分布直方图如图所示，已知第组有人.

    （1）求该组织的人数；

    （2）若在第组中用分层抽样的方法抽取名志愿者参加某社区的宣传活动，应从第组各抽取多少名志愿者？

    （3）在（2）的条件下，该组织决定在这名志愿者中随机抽取名志愿者介绍宣传经验，求第组至少有名志愿者被抽中的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下面左图是我省某地斜拉式大桥的图片，合肥一中学数学兴趣小组对大桥有关数据进行了测量，并将其简化为右图所示.其中桥塔AB，CD与桥面AC垂直，若.

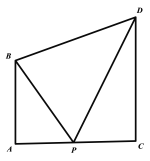
    （1）当时，试确定点P在线段AC上的位置，并写出求解过程；

    （2）要使得达到最大，试问点P在线段AC上何处？请写出求解过程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下表是某公司2018年5~12月份研发费用（百万元）和产品销量（万台）的具体数据：

    月 份

    5

    6

    7

    8

    9

    10

    11

    12

    研发费用（百万元）

    2

    3

    6

    10

    21

    13

    15

    18

    产品销量（万台）

    1

    1

    2

    2.5

    6

    3.5

    3.5

    4.5

    （Ⅰ）根据数据可知与之间存在线性相关关系，求出与的线性回归方程（系数精确到0.01）；

    （Ⅱ）该公司制定了如下奖励制度：以（单位：万台）表示日销售，当时，不设奖；当时，每位员工每日奖励200元；当时，每位员工每日奖励300元；当时，每位员工每日奖励400元.现已知该公司某月份日销售（万台）服从正态分布（其中是2018年5-12月产品销售平均数的二十分之一），请你估计每位员工该月（按30天计算）获得奖励金额总数大约多少元.

    参考数据：，，，，

    参考公式：相关系数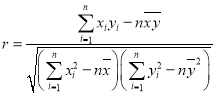，其回归直线中的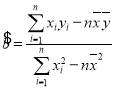，若随机变量服从正态分布，则，.

    查看答案和解析>>

    同步练习册答案