【题目】设函数
在区间
上单调递减，则实数
的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】∵
，
∴
，
由
得
，
∴函数
的单调减区间为
，
又函数
在区间
上单调递减，
∴
，
∴
，解得
，
∴实数
的取值范围是
．选C．
点睛：已知函数在区间上的单调性求参数的方法
（1）利用导数求解，转化为导函数在该区间上大于等于零（或小于等于零）恒成立的问题求解，一般通过分离参数化为求函数的最值的问题．
（2）先求出已知函数的单调区间，然后将问题转化为所给的区间是函数相应的单调区间的子集的问题处理．
【题型】单选题
【结束】
7
【题目】设
，函数
的图象向右平移
个单位长度后与原图象重合，则
的最小值是（ ）
A. 
B. 
C. 
D. 
名师点拨卷系列答案
英才计划期末调研系列答案科目：高中数学 来源： 题型：
【题目】已知直线l：y=﹣x+1与椭圆C： 
=1（a＞b＞0））相交于不同的两点A、B，且线段AB的中点P的坐标为（ 
， 
） 
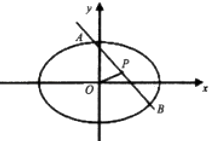
（1）求椭圆C离心率；
（2）设O为坐标原点，且2|OP|=|AB|，求椭圆C的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列有关命题的说法中错误的是
A. 在频率分布直方图中，中位数左边和右边的直方图的面积相等 .
B. 一个样本的方差是
，则这组数据的总和等于60.
C. 在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越差.
D. 对于命题
使得
＜0，则
，使
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】我们为了探究函数
的部分性质，先列表如下：
| … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.004 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
观察表中
值随
值变化的特点，完成以下的问题.
首先比较容易看得出来：此函数在区间
上是递减的；
（1）函数
在区间 上递增
当
时，
= .
（2）请你根据上面性质作出此函数的大概图像；
（3）试用函数单调性的定义证明：函数
在区间上为减函数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】宜昌市拟在2020年点军奥体中心落成后申办2022年湖北省省运会，据了解，目前武汉，襄阳，黄石等申办城市因市民担心赛事费用超支而准备相继退出，某机构为调查宜昌市市民对申办省运会的态度，选了某小区的100位居民调查结果统计如下：
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
（1）根据已知数据，把表格数据填写完整；
（2）能否在犯错误的概率不超过
的前提下认为不同年龄与支持申办省运会无关？
（3）已知在被调查的年龄大于50岁的支持者中有5名女性，其中2位是女教师，现从这5名女性中随机抽取3人，求至多有1位教师的概率．
附：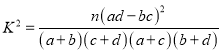 
, 
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
