
���� ��1������֪�ã�С���н��ĸ���Ϊ$\frac{2}{3}$��С���н��ĸ���Ϊ$\frac{2}{5}$���������н����Ӱ�죮�ǡ���2�˵��ۼƵ÷�X��3�����¼�ΪA�����¼�A�����С�X=0������X=2������X=3����������������¼����ɴ��������2�˵��ۼƵ÷�X��3�ĸ��ʣ�
��2����С����С�춼ѡ��������õ��ۼƵ÷�ΪX1������֪��X1�����п���ȡֵΪ0��2��4���ֱ������Ӧ�ĸ��ʣ��ɴ������X1�ķֲ��к�E��X1����С����С�춼ѡ��������õ��ۼƵ÷�ΪX2������֪��X2�����п���ȡֵΪ0��3��6���ֱ������Ӧ�ĸ��ʣ��ɴ������X2�ķֲ��к�E��X2�����Ӷ��õ����Ƕ�ѡ������Ͷ��ʱ���ۼƵ÷ֵ���ѧ�����ϴ�
��� ����������12�֣�
�⣺��1������֪�ã�С���н��ĸ���Ϊ$\frac{2}{3}$��С���н��ĸ���Ϊ$\frac{2}{5}$��
�������н����Ӱ�죮�ǡ���2�˵��ۼƵ÷�X��3�����¼�ΪA��
���¼�A�����С�X=0������X=2������X=3����������������¼�������1�֣�
��ΪP��X=0��=��1-$\frac{2}{3}$������1-$\frac{2}{5}$��=$\frac{1}{5}$��
P��X=2��=$\frac{2}{3}$����1-$\frac{2}{5}$��=$\frac{2}{5}$��
P��X=3��=��1-$\frac{2}{3}$����$\frac{2}{5}$=$\frac{2}{15}$��
����P��A��=P��X=0��+P��X=2��+P��X=3��=$\frac{11}{15}$��
����2�˵��ۼƵ÷�X��3�ĸ���Ϊ$\frac{11}{15}$������5�֣�
��2����С����С�춼ѡ��������õ��ۼƵ÷�ΪX1������֪��X1�����п���ȡֵΪ0��2��4��
P��X1=0��=$\frac{1}{3}��\frac{1}{3}$=$\frac{1}{9}$��
P��X1=2��=$\frac{2}{3}��\frac{1}{3}+\frac{1}{3}��\frac{2}{3}$=$\frac{4}{9}$��
P��X1=4��=$\frac{2}{3}��\frac{2}{3}$=$\frac{4}{9}$��
��X1�ķֲ������£�
| X1 | 0 | 2 | 4 |
| P | $\frac{1}{9}$ | $\frac{4}{9}$ | $\frac{4}{9}$ |
| X2 | 0 | 3 | 6 |
| P | $\frac{9}{25}$ | $\frac{12}{25}$ | $\frac{4}{25}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע��������¼����ʳ˷���ʽ�ĺ������ã�


 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
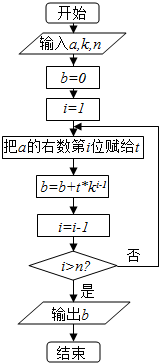 ִ����ͼ��ʾ�ij����ͼ��������a=110011��k=2��n=6���������b��ֵ�ǣ�������
ִ����ͼ��ʾ�ij����ͼ��������a=110011��k=2��n=6���������b��ֵ�ǣ�������| A�� | 102 | B�� | 49 | C�� | 50 | D�� | 51 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{945}$ | B�� | $\frac{4}{63}$ | C�� | $\frac{8}{63}$ | D�� | $\frac{16}{63}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1��2��3��4} | B�� | {2��3��4} | C�� | {2��4} | D�� | {x|1��x��4} |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com