已知定义域为R(实数集)的函数,f(x)中,f(0)=1
且当n-1≤x<n(n∈Z)时,f(x)=(x-n)•f(n-1)+f(n)
(Ⅰ)求f(2)的值及当x∈[3,4)时,f(x)的表达式;
(Ⅱ)判断函数f(x)的单调性,并说明理由;
(Ⅲ)“定义:设g(x)为定义在D上的函数,若存在正数M,对任意x∈D都有|g(x)|≤M,则称函数g(x)为D上有界函数;否则,称函数g(x)为D上无界函数.”试证明f(x)为R上无界函数.
解:(Ⅰ)由题意得f(0)=(0-1)f(0)+f(1),
∵f(0)=1∴f(1)=2
同理得:∴f(2)=4(2分)
又对任意n∈Z,f(n)=(n-n-1)f(n)+f(n+1)
即 2f(n)=f(n+1)(4分)
当n∈N
+时,f(n)=2f(n-1)=2
2f(n-2)=…=2
nf(0)=2
n当n∈N
-时,f(0)=2f(-1)=2
2f(-2)=…=2
-nf(n),
即 f(n)=2
n. (7分)
综上可得:f(n)=2
n(n∈Z)
当x∈[3,4)时,f(x)=f(3)(x-4)+f(4)=8x-16(8分)
(Ⅱ)f(x)是定义域上的增函数.
任意取两个实数x
1,x
2,设x
1<x
2①若n-1≤x
1<x
2<n,则f(x
1)-f(x
2)=f(n-1)(x
1-n)+f(n)-f(n-1)(x
2-n)-f(n)
=f(n-1)(x
1-x
2)=2
n-1(x
1-x
2)<0(12分)
②若n
1-1则x
1<n
1n-1<x
2<n,
依①可得 f(x
2)…f(n-1)
事实上 f(n-1)=2
n-1,
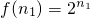
,∵n
1,n-1
∴f(n
1),f(n-1)∴f(x
2)≥f(n
1)
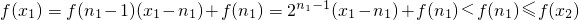
综上所述:f(x
1)<f(x
2)(16分)
所以,f(x)是定义域上的增函数.
(Ⅲ)对任意M>0,取M
0>M,且log
2M
0∈Z,
记x
0=log
2M
0则:
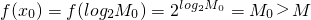
所以 f(x)为R上无界函数. (20分)
分析:(Ⅰ)令x=0,求出f(1)的值,进而得出f(2)的值;令x=n,得出2f(n)=f(n+1),进而求出当n∈N
+时,f(n)=2
n,当n∈N
-时,f(n)=2
n,即可求出f(x)的表达式.
(Ⅱ)取两个实数x
1,x
2,设x
1<x
2,①若n-1≤x
1<x
2<n,则f(x
1)-f(x
2)=2
n-1(x
1-x
2)<0;若n
1-1则x
1<n
1n-1<x
2<n,f(x
2)≥f(n
1)
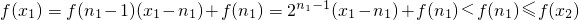
,即可得出结果.
(Ⅲ)对任意M>0,取M
0>M,且log
2M
0∈Z,记x
0=log
2M
0,则:f(x
0)=2
log2M0=M
0>M,即可得出结论.
点评:本题考查了函数单调性的判断和证明以及函数的恒成立问题,此题的难度较大,要认真审题,仔细作答.

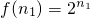 ,∵n1,n-1
,∵n1,n-1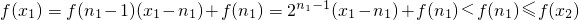
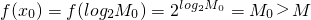
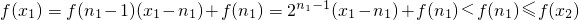 ,即可得出结果.
,即可得出结果.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案