
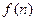 表示前
表示前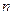 年的纯利润总和,
年的纯利润总和, 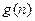 表示前
表示前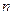 年的总支出.
年的总支出. 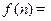 前
前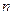 年的总收入-前
年的总收入-前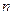 年的总支出-投资额].
年的总支出-投资额].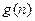 的关系式
的关系式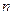 年的纯利润总和
年的纯利润总和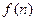 关于
关于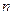 的函数关系式;并求该厂从第几年开始盈利?
的函数关系式;并求该厂从第几年开始盈利? 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源:不详 题型:解答题
 的厂房(不管墙高),工程的造价是:
的厂房(不管墙高),工程的造价是:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
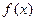 ,若存在x0∈R,使
,若存在x0∈R,使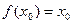 成立,则称x0为
成立,则称x0为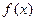 的不动点。已知函数
的不动点。已知函数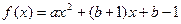 (a≠0)。
(a≠0)。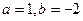 时,求函数
时,求函数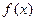 的不动点;
的不动点;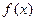 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;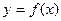 图象上A、B两点的横坐标是函数
图象上A、B两点的横坐标是函数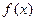 的不动点,且A、B两点关于点
的不动点,且A、B两点关于点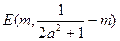 对称,求
对称,求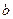 的的最小值。
的的最小值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (
( 2),BC=2,且AE=AH=CF=CG,设AE=
2),BC=2,且AE=AH=CF=CG,设AE= ,绿地面积为
,绿地面积为 .
. 关于
关于 的函数关系式,指出这个函数的定义域.
的函数关系式,指出这个函数的定义域.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 的定义域;
的定义域; 的图象上是否存在不同的两点,使过这两点的直线平行于
的图象上是否存在不同的两点,使过这两点的直线平行于 轴;
轴; 满足什么条件时,
满足什么条件时, 在
在 上恒取正值.
上恒取正值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,政府补贴为
,政府补贴为 。根据市场调查,当
。根据市场调查,当 时,淡水鱼的
时,淡水鱼的 市场日供应
市场日供应 量
量 与市场日需求量
与市场日需求量 近似满足关系:
近似满足关系: ,
, ;当
;当 时的市场价格称为市场平衡价格。
时的市场价格称为市场平衡价格。 ,政府需要补贴吗?如果需要,至少为多少
,政府需要补贴吗?如果需要,至少为多少 ?
?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 +r=0的解集分别为A、B且A≠B,A∪B={-3,4 },A∩B={-3},求p,q,r的值.
+r=0的解集分别为A、B且A≠B,A∪B={-3,4 },A∩B={-3},求p,q,r的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com