
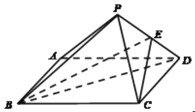
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的动点.记
的动点.记![]() 与
与![]() 所成角的最小值为
所成角的最小值为![]() ,当
,当![]() 为线段
为线段![]() 中点时,二面角
中点时,二面角![]() 的大小为
的大小为![]() ,二面角
,二面角![]() 的大小为
的大小为![]() ,则
,则![]() ,
,![]() ,
,![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() (a>b>0)过点E(
(a>b>0)过点E(![]() ,1),其左、右顶点分别为A,B,左、右焦点为F1,F2,其中F1(
,1),其左、右顶点分别为A,B,左、右焦点为F1,F2,其中F1(![]() ,0).
,0).
(1)求椭圆C的方程:
(2)设M(x0,y0)为椭圆C上异于A,B两点的任意一点,MN⊥AB于点N,直线l:x0x+2y0y﹣4=0,设过点A与x轴垂直的直线与直线l交于点P,证明:直线BP经过线段MN的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某学校研究性课题《什么样的活动最能促进同学们进行垃圾分类》向题的统计图(每个受访者都只能在问卷的5个活动中选择一个),以下结论错误的是( )

A. 回答该问卷的总人数不可能是100个
B. 回答该问卷的受访者中,选择“设置分类明确的垃圾桶”的人数最多
C. 回答该问卷的受访者中,选择“学校团委会宣传”的人数最少
D. 回答该问卷的受访者中,选择“公益广告”的人数比选择“学校要求”的少8个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上的点到准线的最小距离为2.
上的点到准线的最小距离为2.
(1)求抛物线![]() 的方程;
的方程;
(2)若过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,
,![]() ,
,![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() 分别为弦
分别为弦![]() ,
,![]() 的中点,求
的中点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将1,2,3,……,9这9个数全部填入如图所示的3×3方格内,每个格内填一个数,则使得每行中的数从左至右递增,每列中的数从上至下递减的不同填法共有( )种
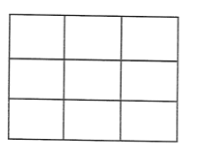
A.12B.24C.42D.48
查看答案和解析>>
科目:高中数学 来源: 题型:
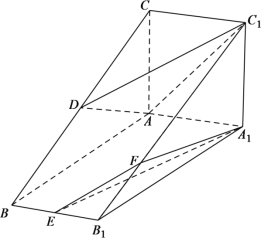
【题目】如图,在三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 是正方形,点
是正方形,点![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)若点![]() 在棱
在棱![]() 上,且
上,且![]() ,判断平面
,判断平面![]() 与平面
与平面![]() 是否平行,并说明理由.
是否平行,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,函数的图象沿
,函数的图象沿![]() 轴向右平移
轴向右平移![]() 个单位长度后关于
个单位长度后关于![]() 轴对称,则下列结论正确的是______.(填序号)
轴对称,则下列结论正确的是______.(填序号)
①![]() 是函数
是函数![]() 图象的一个对称中心;
图象的一个对称中心;
②![]() 在区间
在区间![]() 上的最小值为-2;
上的最小值为-2;
③![]() 的单调递增区间是
的单调递增区间是![]() ;
;
④函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 时只有一个交点.
时只有一个交点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com