
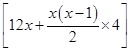 =-2x2+40x-98,令y>0,得10-
=-2x2+40x-98,令y>0,得10-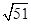 <x<10+
<x<10+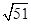 ,∵x∈N*,∴3≤x≤17.即引进该设备三年后开始盈利--- 6分
,∵x∈N*,∴3≤x≤17.即引进该设备三年后开始盈利--- 6分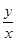 ,
,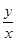 =-2x-
=-2x-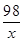 +40≤-2
+40≤-2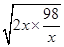 +40=12,当且仅当2x=
+40=12,当且仅当2x=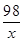 ,即x=7时,年平均利润最大,共盈利12×7+26=110万元--------------9分
,即x=7时,年平均利润最大,共盈利12×7+26=110万元--------------9分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com