
思路分析:定积分的概念产生于分割、近似代替、求和、取极限这四步.故用四步法求定积分要注意解题的层次性,当然本题省略了求极限这一步.
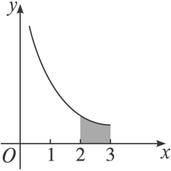
解:在[2,3]上等间隔地插入n-1个点,将它等分成几个小区间[2,2+![]() ],[2+
],[2+![]() ,2+
,2+![]() ],…,[2+
],…,[2+![]() ,3],记第i个区间为[2+
,3],记第i个区间为[2+![]() ,2+
,2+![]() ](i=1,2,…,n),其长度为Δx=
](i=1,2,…,n),其长度为Δx=![]() .
.
分别过上述n-1个分点作x轴的垂线,把曲边梯形分成n个小曲边梯形,它们的面积分别为ΔS1、ΔS2、…ΔSn,显然S=![]() ,设f(x)=
,设f(x)=![]() ,如图1-5-4所示,当n很大时,Δx很小,在区间[2+
,如图1-5-4所示,当n很大时,Δx很小,在区间[2+![]() ,2+
,2+![]() ]上,可以认为函数f(x)=
]上,可以认为函数f(x)=![]() 的值变化很小,近似地等于一个常数,不妨认为它近似地等于ξi=
的值变化很小,近似地等于一个常数,不妨认为它近似地等于ξi=![]() 处的函数值f(ξi)=
处的函数值f(ξi)=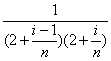 ,这样在区间[2+
,这样在区间[2+![]() ,2+
,2+![]() ]上,用小矩形面积ΔSi′近似地代替ΔSi,则有ΔSi≈ΔSi′=f(ξi)·Δx
]上,用小矩形面积ΔSi′近似地代替ΔSi,则有ΔSi≈ΔSi′=f(ξi)·Δx
= ·
·![]() (i=1,2,…,n).
(i=1,2,…,n).
∴Sn=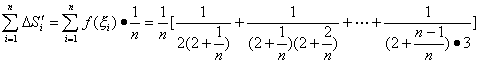


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com