
【题目】设直线![]() 与圆
与圆![]() 交于M、N两点,且M、N关于直线
交于M、N两点,且M、N关于直线![]() 对称.
对称.
(1)求m,k的值;
(2)若直线![]() 与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
与圆C交P,Q两点,是否存在实数a使得OP⊥OQ,如果存在,求出a的值;如果不存在,请说明理由.
【答案】(1)![]() (2)不存在.
(2)不存在.
【解析】试题分析:(1)由M,N关于直线x+y=0对称,可知所求的直线的斜率k=1,根据圆的性质可得直线y+x=0过圆的圆心C(1,m)代入可求m
(2)把x=ay+1代入(x-1)2+(y+1)2=9得(1+a2)y2+2y-8=0,设P(x1,y1),Q(x2,y2),利用韦达定理,OP⊥OQ,则有x1x2+y1y2=0,代入整理可求.
试题解析:
(1)因为圆上的两点![]() 关于直线
关于直线![]() 对称,所以,直线
对称,所以,直线![]() 过圆心,圆心
过圆心,圆心![]() ,即有
,即有![]() ,同时,对称点
,同时,对称点![]() 的连线被对称轴垂直平分,所以又有
的连线被对称轴垂直平分,所以又有![]() ,从而
,从而![]()
(2)由(1)知:圆C(x-1)2+(y+1)2=9,把![]() 代入
代入![]()
得![]() ,设
,设![]() , 则
, 则![]() ,
,![]()
若![]() ,则有x1x2+y1y2=0,
,则有x1x2+y1y2=0, ![]()
![]()
![]()
即![]() , 方程无实数根,所以满足条件的实数
, 方程无实数根,所以满足条件的实数![]() 不存在.
不存在.


科目:高中数学 来源: 题型:
【题目】某种药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材的收益,若基地收益如下表所示:已知下周一和下周二无雨的概率相同且为![]() ,两天是否下雨互不影响,若两天都下雨的概率为
,两天是否下雨互不影响,若两天都下雨的概率为![]()

(1)求![]() 及基地的预期收益;
及基地的预期收益;
(2)若该基地额外聘请工人,可在周一当天完成全部采摘任务,若周一无雨时收益为![]() 万元,有雨时收益为
万元,有雨时收益为![]() 万元,且额外聘请工人的成本为
万元,且额外聘请工人的成本为![]() 元,问该基地是否应该额外聘请工人,请说明理由.
元,问该基地是否应该额外聘请工人,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的一点,且
上的一点,且![]() .现将四边形
.现将四边形![]() 沿直线
沿直线![]() 翻折,使翻折后的二面角
翻折,使翻折后的二面角![]() 的余弦值为
的余弦值为![]() .
.
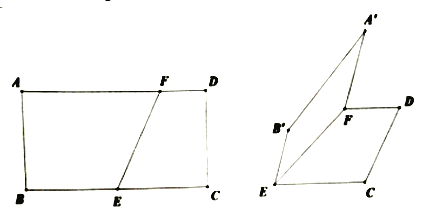
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DBEC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面, ![]() ,
, ![]() .
.
(1)若![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(2)证明:平面ACD⊥平面BCDE;
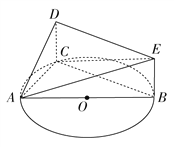
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照国家环保部发布的新修订的《环境空气质量标准》,规定:PM2.5的年平均浓度不得超过35微克/立方米,国家环保部门在2016年10月1日到2017年1月30日这120天对全国的PM2.5平均浓度的监测数据统计如下:
组别 | PM2.5浓度(微克/立方米) | 频数(天) |
第一组 |
| 32 |
第二组 |
| 64 |
第三组 |
| 16 |
第四组 | 115以上 | 8 |
(1)在这120天中抽取30天的数据做进一步分析,每一组应抽取多少天?
(2)在(1)中所抽取的样本PM2.5的平均浓度超过75(微克/立方米)的若干天中,随机抽取2天,求恰好有一天平均浓度超过115(微克/立方米)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com