
【题目】已知集合![]() ,集合
,集合![]() .
.
![]() 当
当![]() 时,求
时,求![]() ;
;
![]() ,不等式
,不等式![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
![]() 若“
若“![]() ”是“
”是“![]() ”的必要条件,求实数a的取值范围.
”的必要条件,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
![]() 根据题意,当
根据题意,当![]() 时,求出集合A、B,由交集的定义计算可得答案;
时,求出集合A、B,由交集的定义计算可得答案;
![]() 根据题意,设
根据题意,设![]() ,结合二次函数的性质分析可得
,结合二次函数的性质分析可得![]() ,解可得
,解可得![]() 的取值范围,即可得答案;
的取值范围,即可得答案;
![]() 根据题意,分
根据题意,分![]() 种情况讨论:
种情况讨论:![]() ,当
,当![]() ,即
,即![]() 或2时,
或2时,![]() ,
,![]() ,当
,当![]() ,即
,即![]() 或
或![]() 时,
时,![]() ,
,![]() ,当
,当![]() ,即
,即![]() 时,
时,![]() ,分别求出
,分别求出![]() 的取值范围,综合即可得答案.
的取值范围,综合即可得答案.
解:![]() 根据题意,
根据题意,
当![]() 时,
时,![]() ;
;
集合![]() .
.
则![]() ;
;
![]() 根据题意,设
根据题意,设![]() ,
,
若![]() ,不等式
,不等式![]() ,
,
必有![]() ,
,
解可得:![]() ,
,
即实数a的取值范围是![]() ;
;
![]() 根据题意,分3种情况讨论:
根据题意,分3种情况讨论:
![]() ,当
,当![]() ,即
,即![]() 或2时,
或2时,![]() ,
,![]() ,“
,“![]() ”是“
”是“![]() ”的必要条件,符合题意;
”的必要条件,符合题意;
![]() ,当
,当![]() ,即
,即![]() 或
或![]() 时,
时,
![]() ,若“
,若“![]() ”是“
”是“![]() ”的必要条件,则必有
”的必要条件,则必有![]() ,
,
解可得:![]() 或
或![]() ;
;
![]() ,当
,当![]() ,即
,即![]() 时,
时,
![]() ,若“
,若“![]() ”是“
”是“![]() ”的必要条件,则必有
”的必要条件,则必有![]() ,
,
此时无解;
综合可得:![]() 或
或![]() ;
;
故a的取值范围为![]() 或
或![]()


科目:高中数学 来源: 题型:
【题目】点P在双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的右支上,其左、右焦点分别为F1 , F2 , 直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2 , 则该双曲线的渐近线的斜率为 .
=1(a>0,b>0)的右支上,其左、右焦点分别为F1 , F2 , 直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2 , 则该双曲线的渐近线的斜率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx+ax﹣ ![]() (a∈R)在x=2处的切线经过点(﹣4,ln2)
(a∈R)在x=2处的切线经过点(﹣4,ln2)
(1)讨论函数f(x)的单调性;
(2)若不等式 ![]() >mx﹣1恒成立,求实数m的取值范围.
>mx﹣1恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了缓解城市交通压力,大力发展公共交通,提倡多坐公交少开车,为了调查市民乘公交车的候车情况,交通主管部门从在某站台等车的![]() 名候车乘客中随机抽取
名候车乘客中随机抽取![]() 人,按照他们的候车时间(单位:分钟)作为样本分成
人,按照他们的候车时间(单位:分钟)作为样本分成![]() 组,如下表所示:
组,如下表所示:
组别 | 一 | 二 | 三 | 四 | 五 | 六 |
候车时间 |
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
(1)估计这![]() 名乘客中候车时间少于
名乘客中候车时间少于![]() 分钟的人数;
分钟的人数;
(2)若从上表第四、五组的![]() 人中随机抽取
人中随机抽取![]() 人做进一步的问卷调查,求抽到的
人做进一步的问卷调查,求抽到的![]() 人恰好来自不同组的概率.
人恰好来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12.若曲线C的左焦点F在直线l上,且直线l与曲线C交于A,B两点.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12.若曲线C的左焦点F在直线l上,且直线l与曲线C交于A,B两点.
(1)求m的值并写出曲线C的直角坐标方程;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义[x]表示不超过的最大整数,如[2]=2,[2,2]=2,执行如图所示的程序框图,则输出S=( ) 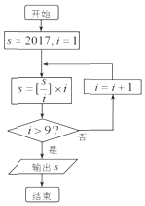
A.1991
B.2000
C.2007
D.2008
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com