
【题目】已知函数![]() ,
,
(1)若函数![]() 的图像上有与
的图像上有与![]() 轴平行的切线,求参数
轴平行的切线,求参数![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 处取得极值,且
处取得极值,且![]() 时,
时,![]() 恒成立,求参数
恒成立,求参数![]() 的取值范围.
的取值范围.
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】在空间中,下列命题正确的是
A.如果一个角的两边和另一角的两边分别平行,那么这两个角相等
B.两条异面直线所成的有的范围是![]()
C.如果两个平行平面同时与第三个平面相交,那么它们的交线平行
D.如果一条直线和平面内的一条直线平行,那么这条直线和这个平面平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,对称轴为坐标轴,椭圆
的中心在原点,对称轴为坐标轴,椭圆![]() 与直线
与直线![]() 相切于点
相切于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点(
两点(![]() ,
, ![]() 不是长轴端点),且以
不是长轴端点),且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 在
在![]() 轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.
轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网的快速发展,基于互联网的共享单车应运而生,某市场研究人员为了了解共享单车运营公司![]() 的经营状况,对该公司最近六个月的市场占有率进行了统计,并绘制了相应的折线图:
的经营状况,对该公司最近六个月的市场占有率进行了统计,并绘制了相应的折线图:
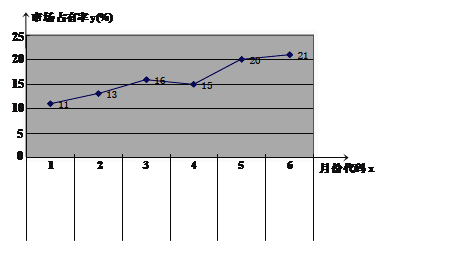
(1)由折线图可以看出,可用线性回归模型拟合月度市场占有率![]() 与月份代码
与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并
的线性回归方程,并
预测![]() 公司2017年4月的市场占有率;
公司2017年4月的市场占有率;
(2)为进一步扩大市场,公司拟再采购一批单车,现有采购成本分别为![]() 元/辆和1200元/辆的
元/辆和1200元/辆的![]() 、
、![]() 两款车型可供选择,按规定每辆单车最
两款车型可供选择,按规定每辆单车最
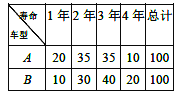
多使用4年,但由于多种原因(如骑行频率等)会导致单车使用寿命各不相同,考虑到公司运营的经济效益,该公司决定先对这两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命的频数表如右表:经测算,平均每辆单车每年可以带来收入500元,不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率,如果你是![]() 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
参考公式:回归直线方程为![]() ,其中
,其中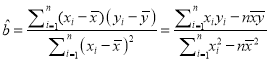 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C: ![]() ,过点
,过点![]() 的直线l的参数方程为:
的直线l的参数方程为: 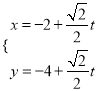 (t为参数),直线l与曲线C分别交于M、N两点.
(t为参数),直线l与曲线C分别交于M、N两点.
(1)写出曲线C的直角坐标方程和直线l的普通方程;
(2)若|PM |,|MN|,|PN|成等比数列,求a的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地有一企业2007年建厂并开始投资生产,年份代号为7,2008年年份代号为8,依次类推.经连续统计9年的收入情况如下表(经数据分析可用线性回归模型拟合![]() 与
与![]() 的关系):
的关系):
年份代号( | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
当年收入( | 13 | 14 | 18 | 20 | 21 | 22 | 24 | 28 | 29 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)试预测2020年该企业的收入.
(参考公式: 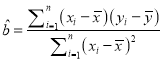
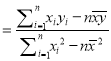 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为![]() (
(![]() ).
).
(1)若直线l在两坐标轴上的截距相等,求直线l的方程;
(2)若直线l与x正半轴、射线![]() (
(![]() )分别交于P,Q两点,当a为何值时,
)分别交于P,Q两点,当a为何值时,![]() 的面积最小?
的面积最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com