
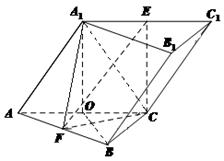
如图,斜三棱柱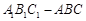 中,侧面
中,侧面
 底面ABC,底面ABC是边长为2的等边三角形,侧面
底面ABC,底面ABC是边长为2的等边三角形,侧面 是菱形,
是菱形,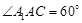 ,E、F分别是
,E、F分别是 、AB的中点.
、AB的中点.

求证:(1) ;
;
(2)求三棱锥 的体积.
的体积.
(1)证明详见解析;(2)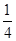
【解析】
试题分析:(1)作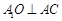 ,O为垂足,而
,O为垂足,而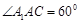 ,可证O为AC的中点,得
,可证O为AC的中点,得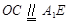 ,可证四边形
,可证四边形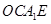 为平行四边形,即
为平行四边形,即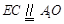 ,由已知可得
,由已知可得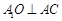 ,所以
,所以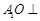 底面ABC.即
底面ABC.即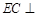 底面ABC.
底面ABC.
(2)由于底面ABC是等边三角形,且F是AB的中点,可知F到平面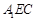 的距离等于B点到平面
的距离等于B点到平面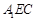 距离BO的一半,而BO=
距离BO的一半,而BO=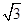 ,又三棱锥
,又三棱锥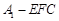 的体积等于三棱锥F-EA1C的体积,求出三角形EA1C的面积,最后根据棱锥的体积公式求解即可.
的体积等于三棱锥F-EA1C的体积,求出三角形EA1C的面积,最后根据棱锥的体积公式求解即可.
试题解析:证明:(1)
在平面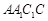 内,作
内,作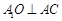 ,O为垂足.
,O为垂足.
因为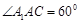 ,所以
,所以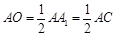 ,即O为AC的中点,所以
,即O为AC的中点,所以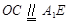 .
3分
.
3分
因而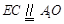 .因为侧面
.因为侧面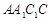 ⊥底面ABC,交线为AC,
⊥底面ABC,交线为AC,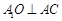 ,所以
,所以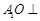 底面ABC.
底面ABC.
所以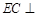 底面ABC.
6分
底面ABC.
6分
(2)F到平面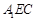 的距离等于B点到平面
的距离等于B点到平面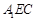 距离BO的一半,而BO=
距离BO的一半,而BO=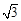 .
8分
.
8分
所以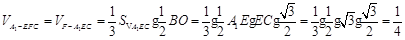 .
12分
.
12分
考点:平面与平面垂直的性质、直线与平面垂直的判定以及棱锥的体积.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
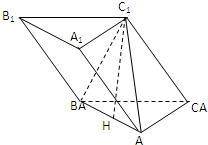 如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.
如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.查看答案和解析>>
科目:高中数学 来源: 题型:
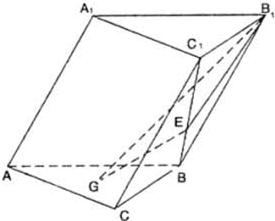 如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2,低面ABC是边长为2的正三角形,其重心为G点(重心为三条中线的交点).E是线段BC1上一点且BE=
如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2,低面ABC是边长为2的正三角形,其重心为G点(重心为三条中线的交点).E是线段BC1上一点且BE=| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
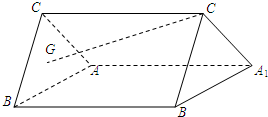 (2008•成都二模)如图,斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面ABB1A1,AC=AB=
(2008•成都二模)如图,斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面ABB1A1,AC=AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
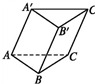 如图,斜三棱柱ABC-A′B′C′中,底面是边长为a的正三角形,侧棱长为b,侧棱AA′与底面相邻两边AB,AC都成45°角.
如图,斜三棱柱ABC-A′B′C′中,底面是边长为a的正三角形,侧棱长为b,侧棱AA′与底面相邻两边AB,AC都成45°角.查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)如图,斜三棱柱![]() 中,
中,![]() 在底面的射影
在底面的射影![]() 恰好是
恰好是![]() 的中点,侧棱与底面成
的中点,侧棱与底面成![]() 角,侧面
角,侧面![]() 与侧面
与侧面![]() 成
成![]() 角.
角.
(1)求证:四边形![]() 是矩形;(2)求斜三棱柱
是矩形;(2)求斜三棱柱![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com