
【题目】对一堆100粒的石子进行如下操作:每次任选石子数大于1的一堆任意分成不空的两堆,直到每堆1粒(100堆)为止.证明:
(1)无论如何操作,必有某个时刻存在20堆,其石子总数为60;
(2)可以进行适当地操作使得任何时刻不存在19堆,其石子总数为60.
【答案】(1)见解析;(2)见解析
【解析】
(1)易知,19步后石子分成20堆,记此以后第![]() 步操作后粒数最多的20堆之和为
步操作后粒数最多的20堆之和为![]() .
.
显然,![]() 单调不增.
单调不增.
若不存在![]() ,则
,则![]() ,而
,而![]() .
.
设![]() 中各堆的粒数为
中各堆的粒数为![]() ,其中,某个
,其中,某个![]() 分裂成两堆
分裂成两堆![]() ,重排后得
,重排后得![]() 的各堆的粒数为
的各堆的粒数为![]() .则
.则![]() .
.
只有三种可能的重排情形.
(i)若![]() ,
,![]() 离开
离开![]() ,
,![]() ,则
,则![]() .
.
(ii)若![]() ,
,![]() 离开
离开![]() ,
,![]() ,则
,则![]() .
.
(iii)若![]() ,
,![]() (
(![]() 是第
是第![]() 步后粒数仅次于
步后粒数仅次于![]() 的堆),则
的堆),则![]() .
.
由于![]() ,只能
,只能![]() ,
,![]() ,
,![]() ,
,![]() .
.
但此时![]() ,故
,故![]() .
.
![]() 之外的各堆粒数均为1或2,总粒数为
之外的各堆粒数均为1或2,总粒数为![]() 为奇数,故必有一堆粒数是1,将其与
为奇数,故必有一堆粒数是1,将其与![]() 交换即得第
交换即得第![]() 步后有20堆,其石子总数为60.
步后有20堆,其石子总数为60.
(2)称初始堆为“主堆”,每步从中分出3粒,33步后成为33个3粒堆和一个1粒堆.该过程中主堆的粒数始终为模3余1,其他堆为3粒.故任意19堆若不含主堆,石子总数为57,而若含主堆,石子总数为模3余1,也不等于60.
此后无论如何操作,由于每堆不多于3粒,任意19堆的石子总数不多于57,因此,任何时刻均不存在19堆,其石子总数为60.


科目:高中数学 来源: 题型:
【题目】某运动员每次射击命中不低于8环的概率为![]() ,命中8环以下的概率为
,命中8环以下的概率为![]() ,现用随机模拟的方法估计该运动员三次射击中有两次命中不低于8环,一次命中8环以下的概率:先用计算器产生0至9之间取整数值的随机数.指定0、1、2、3、4、5表示命中不低于8环,6、7、8、9表示命中8环以下,再以三个随机数作为一组.代表三次射击的结果,产生如下20组随机数:
,现用随机模拟的方法估计该运动员三次射击中有两次命中不低于8环,一次命中8环以下的概率:先用计算器产生0至9之间取整数值的随机数.指定0、1、2、3、4、5表示命中不低于8环,6、7、8、9表示命中8环以下,再以三个随机数作为一组.代表三次射击的结果,产生如下20组随机数:
524207443815510013429966027954
576086324409472796544917460962
据此估计,该运动员三次射击中有两次命中不低于8环,一次命中8环以下的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名射箭选手最近100次射箭所得环数如下表所示.
甲选手100次射箭所得环数
环数 | 7 | 8 | 9 | 10 |
次数 | 15 | 24 | 36 | 25 |
乙选手100次射箭所得环数
环数 | 7 | 8 | 9 | 10 |
次数 | 10 | 20 | 40 | 30 |
以甲、乙两名射箭选手这100次射箭所得环数的频率作为概率,假设这两人的射箭结果相互独立.
(1)若甲、乙各射箭一次,所得环数分别为X,Y,分别求X,Y的分布列并比较![]() 的大小;
的大小;
(2)甲、乙相约进行一次射箭比赛,各射3箭,累计所得环数多者获胜.若乙前两次射箭均得10环,且甲第一次射箭所得环数为9,求甲最终获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,![]() 是以PF为底边的等腰三角形,PA平行于x轴,点
是以PF为底边的等腰三角形,PA平行于x轴,点![]() ,且点P在直线
,且点P在直线![]() 上运动.记点A的轨迹为C.
上运动.记点A的轨迹为C.
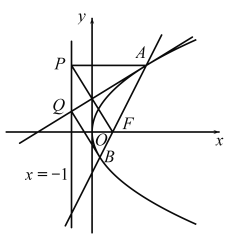
(1)求C的方程.
(2)直线AF与C的另一个交点为B,等腰![]() 底边的中线与直线
底边的中线与直线![]() 的交点为Q,试问
的交点为Q,试问![]() 的面积是否存在最小值?若存在,求出该值;若不存在,请说明理由.
的面积是否存在最小值?若存在,求出该值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个简单图中两两相邻的t个项点称为一个团,与其余每个顶点均相邻的顶点称为中心点.给定整数![]() 及满足
及满足![]() 的整数k,一个n阶简单图G中不存在k+1团,其全部k团记为
的整数k,一个n阶简单图G中不存在k+1团,其全部k团记为![]() .
.
(1)证明:![]() ;
;
(2)若在图G中再添加一条边就存在k+1团,求图G的中心点个数的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com