
【题目】天上有些恒星的亮度是会变化的,其中一种称为造父(型)变星,本身体积会膨胀收缩造成亮度周期性的变化.第一颗被描述的经典造父变星是在1784年.
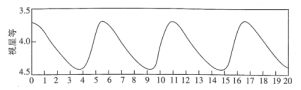
上图为一造父变星的亮度随时间的周期变化图,其中视星等的数值越小,亮度越高,则此变星亮度变化的周期、最亮时视星等,分别约是( )
A.5.5,3.7B.5.4,4.4C.6.5,3.7D.5.5,4.4
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PD=2,DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
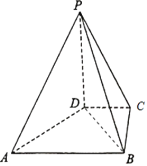
(1)求证:AD⊥PB;
(2)求A点到平面BPC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆锥PO中,AB是圆O的直径,且AB=4,C是底面圆O上一点,且AC=2![]() ,点D为半径OB的中点,连接PD.
,点D为半径OB的中点,连接PD.
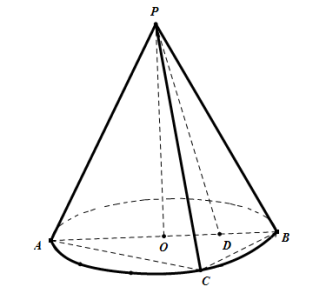
(1)求证:PC在平面APB内的射影是PD;
(2)若PA=4,求底面圆心O到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,对于函数
,对于函数![]() 有下述四个结论:
有下述四个结论:
①函数![]() 在其定义域上为增函数;
在其定义域上为增函数;
②对于任意的![]() ,都有
,都有![]() 成立;
成立;
③![]() 有且仅有两个零点;
有且仅有两个零点;
④若![]() 在点
在点![]() 处的切线也是
处的切线也是![]() 的切线,则
的切线,则![]() 必是
必是![]() 零点.
零点.
其中所有正确的结论序号是( )
A.①②③B.①②C.②③④D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知等边![]() 的边长为3,点
的边长为3,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() .如图2,将
.如图2,将![]() 沿
沿![]() 折起到
折起到![]() 的位置.
的位置.
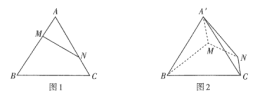
(1)求证:平面![]() 平面
平面![]() ;
;
(2)给出三个条件:①![]() ;②二面角
;②二面角![]() 大小为
大小为![]() ;③
;③![]() .在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段
.在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正△ABC边长为3,点M,N分别是AB,AC边上的点,AN=BM=1,如图1所示.将△AMN沿MN折起到△PMN的位置,使线段PC长为![]() ,连接PB,如图2所示.
,连接PB,如图2所示.
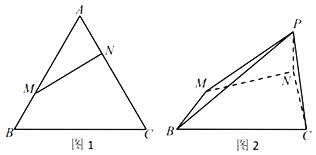
(Ⅰ)求证:平面PMN⊥平面BCNM;
(Ⅱ)若点D在线段BC上,且BD=2DC,求二面角M﹣PD﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com