解:(Ⅰ)∵

,∴f′(x)=mx
2-(4+m)x+4=(mx-4)(x-1)
1)若m>4,则

,此时
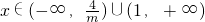
都有
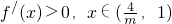
,
有f′(x)<0,∴f(x)的单调递增区间为
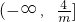
和[[1,+∞);
2)若m=4,则f′(x)=4(x-1)
2≥0,∴f(x)的单调递增区间为(-∞,+∞).
(Ⅱ)当m<0时,
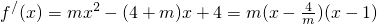
且

∴当2≤x≤3时,都有f′(x)<0
∴此时f(x)在[2,3]上单调递减,∴
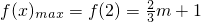
又g(x)=mx+5在[2,3]上单调递减,∴g(x)
min=g(3)=3m+5
∴
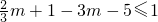
,解得
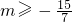
,又m<0,
所以

分析:(1)利用导数研究函数的单调性.由于参数m决定了

与1的大小关系,从而决定导数的正负,因此必须进行分类讨论,通过比较

与1的大小,求出函数的单调增区间;
(2)先假设存在,将对任意的x
1,x
2∈[2,3]都有f(x
1)-g(x
2)≤1转化为f(x)
max-f(x)
min≤1,从而得到关于m的不等式,求出m的取值范围.
点评:利用导数研究含参函数的单调区间,关键是解不等式,因此要研究不等式所对应的方程根的大小,同时应注意对参数的讨论;研究是否存在问题,通常先假设存在,转化为封闭性问题,对于任意性的恒成立问题,一般应利用到函数的最值,而最值的确定又通常利用导数的方法解决.

 mx3-(2+
mx3-(2+ )x2+4x+1,g(x)=mx+5
)x2+4x+1,g(x)=mx+5 ,∴f′(x)=mx2-(4+m)x+4=(mx-4)(x-1)
,∴f′(x)=mx2-(4+m)x+4=(mx-4)(x-1) ,此时
,此时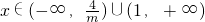 都有
都有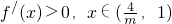 ,
,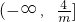 和[[1,+∞);
和[[1,+∞);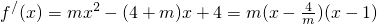 且
且
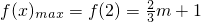
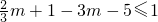 ,解得
,解得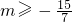 ,又m<0,
,又m<0,
 与1的大小关系,从而决定导数的正负,因此必须进行分类讨论,通过比较
与1的大小关系,从而决定导数的正负,因此必须进行分类讨论,通过比较 与1的大小,求出函数的单调增区间;
与1的大小,求出函数的单调增区间;

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案