
【题目】![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() ,已知
,已知![]() .
.
(1)求![]() ;
;
(2)若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由正弦定理得 sinA=sinBcosC+![]() sinCsinB,从而cosBsinC=
sinCsinB,从而cosBsinC=![]() sinCsinB,进而tanB=
sinCsinB,进而tanB=![]() ,由此能求出B.(2)利用余弦定理得a,由此能求出△ABC的面积.
,由此能求出B.(2)利用余弦定理得a,由此能求出△ABC的面积.
(1)由a=bcosC+![]() csinB及正弦定理,可得:sinA=sinBcosC+
csinB及正弦定理,可得:sinA=sinBcosC+![]() sinCsinB,①
sinCsinB,①
又sinA=sin(π﹣B﹣C)=sin(B+C)=sinBcosC+cosBsinC②,由①②得![]() sinCsinB=cosBsinC,又三角形中,sinC≠0,所以
sinCsinB=cosBsinC,又三角形中,sinC≠0,所以![]() sinB=cosB,又B∈(0,π),所以B=
sinB=cosB,又B∈(0,π),所以B=![]() .
.
(2)△ABC的面积为S=![]() =
=![]() .由余弦定理,b2=a2+c2﹣2accosB,得4=a2+c2﹣
.由余弦定理,b2=a2+c2﹣2accosB,得4=a2+c2﹣![]() ,又
,又![]() ,得c2=4c=2,
,得c2=4c=2,![]() ,所以△ABC的面积为
,所以△ABC的面积为![]() .
.


 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】某单位员工![]() 人参加“学雷锋”志愿活动,按年龄分组:第
人参加“学雷锋”志愿活动,按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
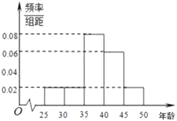
(1)下表是年龄的频率分布表,求正整数![]() 的值;
的值;
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
(2)现在要从年龄较小的第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,年龄在第
人,年龄在第![]() 组抽取的员工的人数分别是多少?
组抽取的员工的人数分别是多少?
(3)在(2)的前提下,从这![]() 人中随机抽取
人中随机抽取![]() 人参加社区宣传交流活动,求至少有
人参加社区宣传交流活动,求至少有![]() 人年龄在第
人年龄在第![]() 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角△ABC中,AB⊥BC,D为BC边上异于B、C的一点,以AB为直径作⊙O,并分别交AC,AD于点E,F.
(Ⅰ)证明:C,E,F,D四点共圆;
(Ⅱ)若D为BC的中点,且AF=3,FD=1,求AE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在对学生的综合素质评价中,将其测评结果分为“优秀、合格、不合格”三个等级,其中不小于80分为“优秀”,小于60分为“不合格”,其它为“合格”. 参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
(1)某校高一年级有男生500人,女生400人,为了解性别对该综合素质评价结果的影响,采用分层抽样的方法从高一学生中抽取45名学生的综合素质评价结果,其各个等级的频数统计如下表:
等级 | 优秀 | 合格 | 不合格 |
男生(人) | 15 | x | 5 |
女生(人) | 15 | 3 | y |
根据表中统计的数据填写下面2×2列联表,并判断是否有90%的把握认为“综合素质评价测评结果为优秀与性别有关”?
优秀 | 男生 | 女生 | 总计 |
非优秀 | |||
总计 |
(2)以(1)中抽取的45名学生的综合素质评价等级的频率作为全市各个评价等级发生的概率,且每名学生是否“优秀”相互独立,现从该市高一学生中随机抽取3人. ①求所选3人中恰有2人综合素质评价为“优秀”的概率;
②记X表示这3人中综合素质评价等级为“优秀”的个数,求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体![]() 中,点
中,点![]() 是棱
是棱![]() 上的一个动点,平面
上的一个动点,平面![]() 交棱
交棱![]() 于点
于点![]() .给出下列命题:
.给出下列命题:
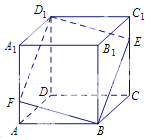
①存在点![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②对于任意的点![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④对于任意的点![]() ,四棱锥
,四棱锥![]() 的体积均不变.
的体积均不变.
其中正确命题的序号是______.(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果直线y=kx+1与圆x2+y2+kx+my﹣4=0交于M、N两点,且M、N关于直线x+y=0对称,则不等式组: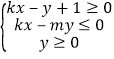 表示的平面区域的面积是( )
表示的平面区域的面积是( )
A.![]()
B.![]()
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪, 图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1).设AD=x(x≥0),DE=y,求用x表示y的函数关系式,并求函数的定义域;
(2).如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆C1的参数方程为![]() (t为参数).以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=4sinθ.
(t为参数).以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=4sinθ.
(1)写出圆C1的极坐标方程,并求圆C1与圆C2的公共弦的长度d;
(2)设射线θ=![]() 与圆C1异于极点的交点为A,与圆C2异于极点的交点为B,求|AB|.
与圆C1异于极点的交点为A,与圆C2异于极点的交点为B,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() 、
、![]() ,并且直线
,并且直线![]() :
: ![]() 平分圆
平分圆![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若过点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 有两个不同的交点
有两个不同的交点![]() .
.
(ⅰ)求实数![]() 的取值范围;
的取值范围;
(ⅱ)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com