
【题目】已知函数f(x)=log2(5﹣x)﹣log2(5+x)+1+m
(1)若f(x)是奇函数,求实数m的值.
(2)若m=0,则是否存在实数x,使得f(x)>2?若存在,求出x的取值范围;若不存在,请说明理由.
【答案】
(1)解:∵f(x)为奇函数,∴f(﹣x)+f(x)=0对定义域中的任意x都成立,
∴log2(5+x)﹣log2(5﹣x)+log2(5﹣x)﹣log2(5+x)+2(1+m)=0,
∴m=﹣1
(2)解:假设存在实数x,使得f(x)>2,
∴log2(5﹣x)﹣log2(5+x)+1>2,
∴log2(5﹣x)>log2(5+x)+1,
∴log2(5﹣x)>log2(5+x)+log22,
∴log2(5﹣x)>log22(5+x),
∴ 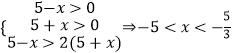 ,
,
∴存在实数 ![]() ,使得f(x)>2
,使得f(x)>2
【解析】1、本题考查的是奇函数的定义,f(x)为奇函数,f(﹣x)+f(x)=0,由定义可得。
2、本题考查的是对数的运算性质,(1)![]() (2)
(2)![]() ,由对数的单调性可得不等式组可得 5 < x <
,由对数的单调性可得不等式组可得 5 < x < ![]() ,使得f(x)>2.
,使得f(x)>2.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数y=f(x)满足f(﹣2)=f(4)=﹣16,且f(x)最大值为2.
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)在[t,t+1](t>0)上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合 A={x|﹣1<x<1},B={x|0<x<2},集合 C={x|x>a}.
(1)求集合A UCRB;
(2)若A∩C≠φ,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】P是双曲线 ![]() =1(a>0,b>0)上的点,F1、F2是其焦点,且
=1(a>0,b>0)上的点,F1、F2是其焦点,且 ![]() =0,若△F1PF2的面积是9,a+b=7,则双曲线的离心率为( )
=0,若△F1PF2的面积是9,a+b=7,则双曲线的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈R,x﹣2>lgx,命题q:x∈R,x2>0,则( )
A.命题p∨q是假命题
B.命题p∧q是真命题
C.命题p∧(¬q)是真命题
D.命题p∨(¬q)是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,AB⊥AD,CD⊥AD,PA⊥平面ABCD,PA=AD=CD=2AB=2,M为PC的中点. (Ⅰ)求证:BM∥平面PAD;
(Ⅱ)平面PAD内是否存在一点N,使MN⊥平面PBD?若存在,确定点N的位置;若不存在,请说明理由.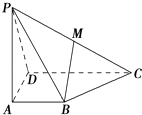
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com