Question

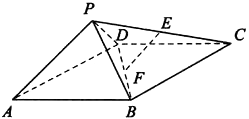
【题目】如图，四棱锥P﹣ABCD中，ABCD为矩形，△PAD为等腰直角三角形，∠APD=90°，面PAD⊥面ABCD，且AB=1，AD=2，E、F分别为PC和BD的中点．
（1）证明：EF∥面PAD；
（2）证明：面PDC⊥面PAD．

Answer 1

【答案】
（1）解：如图，连接AC，

∵ABCD为矩形且F是BD的中点，

∴AC必经过F

又E是PC的中点，

所以，EF∥AP

∵EF在面PAD外，PA在面内，

∴EF∥面PAD

（2）解：∵面PAD⊥面ABCD，CD⊥AD，面PAD∩面ABCD=AD，

∴CD⊥面PAD

又AP面PAD

∴AP⊥CD

又∵AP⊥PD，PD和CD是相交直线，AP⊥面PCD

又AD面PAD，所以，面PDC⊥面PAD

【解析】（1）证明EF∥面PAD，可用线面平行的判定定理，由题设及图，可先证明EF∥AP再由线面平行的判定定理证明；（2）证明面PDC⊥面PAD，由判定定理知要先证明线面垂直，由题设及图知，可先证AP⊥面PCD，再由面面垂直的判定定理证明面面垂直．
【考点精析】掌握直线与平面平行的判定和平面与平面垂直的判定是解答本题的根本，需要知道平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一个平面过另一个平面的垂线，则这两个平面垂直．