练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知奇函数.

    （1）求实数的值；

    （2）判断函数在其定义域上的单调性，并用定义证明；

    （3）若对所有的恒成立，求实数的取值范围.

    【答案】（1）（2）函数是R上的增函数,证明见解析（3）

    【解析】

    （1）根据奇函数性质,可知,代入即可求得的值.

    （2）利用定义,,作差后,将整式变形后即可判断符号,进而判断函数的单调性.

    （3）根据奇函数的性质,结合单调递增,即可将不等式变形为;结合辅助角公式及恒成立问题,解关于m的不等式组即可求得的取值范围.

    （1）若为奇函数,

    则,

    解得.

    （2）由（1）可知,.则是R上的增函数.

    证明：任取,

    则

    且

    即

    所以函数是R上的增函数.

    （3）若对所有的恒成立,

    因为是奇函数,

    对所有的恒成立.

    因为是R上的增函数,

    对所有的恒成立.

    即对所有的恒成立.

    利用辅助角公式变形可得

    因为对所有的恒成立.

    .

    ,

    解得.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】甲、乙、丙、丁四名同学组成一个4100米接力队，老师要安排他们四人的出场顺序，以下是他们四人的要求:甲：我不跑第一棒和第二棒；乙：我不跑第一棒和第四棒；丙：我也不跑第一棒和第四棒；丁：如果乙不跑第二棒，我就不跑第一棒.老师听了他们四人的对话，安排了一种合理的出场顺序，满足了他们的所有要求，据此我们可以断定在老师安排的出场顺序中跑第三棒的人是( )

    A.甲B.乙C.丙D.丁

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在中，已知A，a，b，给出下列说法：

    ①若，则此三角形最多有一解；

    ②若，且，则此三角形为直角三角形，且；

    ③当，且时，此三角形有两解.

    其中正确说法的个数为（ ）

    A.0B.1C.2D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在上的函数的图像关于直线对称，且当时，，过点作曲线的两条切线,若这两条切线互相垂直,则该函数的最小值为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中,已知直线的参数方程为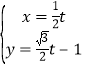（为参数）.在以坐标原点为极点,轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线的极坐标方程是.

    （1）求直线的普通方程与曲线的直角坐标方程；

    （2）设点.若直与曲线相交于两点,求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，.

    （1）当（为自然对数的底数）时，求的极小值；

    （2）讨论函数零点的个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时,讨论函数的单调性；

    （2）当时,若不等式在时恒成立,求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数的图象与曲线C:存在公共切线，则实数的取值范围为

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如城镇小汽车的普及率为75%，即平均每100个家庭有75个家庭拥有小汽车，若从如城镇中任意选出5个家庭，则下列结论成立的是( )

    A.这5个家庭均有小汽车的概率为

    B.这5个家庭中，恰有三个家庭拥有小汽车的概率为

    C.这5个家庭平均有3.75个家庭拥有小汽车

    D.这5个家庭中，四个家庭以上(含四个家庭)拥有小汽车的概率为

    查看答案和解析>>

    同步练习册答案