
【题目】已知函数![]() ,
, ![]() ,(
,( ![]() 为常数)
为常数)
(1)若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() (
(![]() 为常数),求
为常数),求![]() 的值;
的值;
(2)设函数![]() 的导函数为
的导函数为![]() ,若存在唯一的实数
,若存在唯一的实数![]() ,使得
,使得![]() 与
与![]() 同时成立,求实数
同时成立,求实数![]() 的取值范围;
的取值范围;
(3)令![]() ,若函数
,若函数![]() 存在极值,且所有极值之和大于
存在极值,且所有极值之和大于![]() ,求
,求![]() 的取值范围.
的取值范围.
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】某公司租赁甲、乙两种设备生产![]() ,
, ![]() 两类产品,甲种设备每天能生产
两类产品,甲种设备每天能生产![]() 类产品5件和
类产品5件和![]() 类产品10件,乙种设备每天能生产
类产品10件,乙种设备每天能生产![]() 类产品6件和
类产品6件和![]() 类产品20件.已知设备甲每天的租赁费为300元,设备乙每天的租赁费为400元,现该公司至少要生产
类产品20件.已知设备甲每天的租赁费为300元,设备乙每天的租赁费为400元,现该公司至少要生产![]() 类产品50件,
类产品50件, ![]() 类产品140件,则所需租赁费最少为__________元.
类产品140件,则所需租赁费最少为__________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】媒体为调查喜欢娱乐节目![]() 是否与性格外向有关,随机抽取了400名性格外向的和400名性格内向的居民,抽查结果用等高条形图表示如下图:
是否与性格外向有关,随机抽取了400名性格外向的和400名性格内向的居民,抽查结果用等高条形图表示如下图:
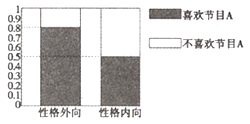
(1)填写完整如下![]() 列联表;
列联表;

(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.001的前提下认为喜欢娱乐节目![]() 与性格外向有关?
与性格外向有关?
参考数据及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
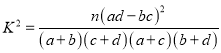
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小组共10人,利用假期参加义工活动,已知参加义工活动1次的有2人,2次的有4人,3次的有4人.现从这10人中随机选出2人作为该组代表参加座谈会.
(1)设![]() 为事件“选出的2人参加义工活动次数之和为4”,求事件
为事件“选出的2人参加义工活动次数之和为4”,求事件![]() 发生的概率;
发生的概率;
(2)设![]() 为选出的2人参加义工活动次数之差的绝对值,求随机变量
为选出的2人参加义工活动次数之差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前![]() 次考试的数学成绩
次考试的数学成绩![]() 、物理成绩进行分析.下面是该生
、物理成绩进行分析.下面是该生![]() 次考试的成绩.
次考试的成绩.
数学 | 108 | 103 | 137 | 112 | 128 | 120 | 132 |
物理 | 74 | 71 | 88 | 76 | 84 | 81 | 86 |
(Ⅰ)他的数学成绩与物理成绩哪个更稳定?请给出你的说明;
(Ⅱ)已知该生的物理成绩![]() 与数学成绩是线性相关的,求物理成绩
与数学成绩是线性相关的,求物理成绩![]() 与数学成绩的回归直线方程
与数学成绩的回归直线方程
(Ⅲ)若该生的物理成绩达到90分,请你估计他的数学成绩大约是多少?
(附: 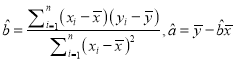 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com