
【题目】已知椭圆![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,椭圆
上,椭圆![]() 的离心率是
的离心率是![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 为椭圆长轴的左端点,
为椭圆长轴的左端点,![]() 为椭圆上异于椭圆
为椭圆上异于椭圆![]() 长轴端点的两点,记直线
长轴端点的两点,记直线![]() 斜率分别为
斜率分别为![]() ,若
,若![]() ,请判断直线
,请判断直线![]() 是否过定点?若过定点,求该定点坐标,若不过定点,请说明理由.
是否过定点?若过定点,求该定点坐标,若不过定点,请说明理由.
【答案】(1)![]() (2)过定点
(2)过定点![]()
【解析】
(1)由点M(﹣1,![]() )在椭圆C上,且椭圆C的离心率是
)在椭圆C上,且椭圆C的离心率是![]() ,列方程组求出a=2,b
,列方程组求出a=2,b![]() ,由此能求出椭圆C的标准方程.
,由此能求出椭圆C的标准方程.
(2)设点P,Q的坐标分别为(x1,y1),(x2,y2),当直线PQ的斜率存在时,设直线PQ的方程为y=kx+m,联立 ,得:(4k2+3)x2+8kmx+(4m2﹣12)=0,利用根的判别式、韦达定理,结合已知条件得直线PQ的方程过定点(1,0);再验证直线PQ的斜率不存在时,同样推导出x0=1,从而直线PQ过(1,0).由此能求出直线PQ过定点(1,0).
,得:(4k2+3)x2+8kmx+(4m2﹣12)=0,利用根的判别式、韦达定理,结合已知条件得直线PQ的方程过定点(1,0);再验证直线PQ的斜率不存在时,同样推导出x0=1,从而直线PQ过(1,0).由此能求出直线PQ过定点(1,0).
(1)由点![]() 在椭圆
在椭圆![]() 上,且椭圆
上,且椭圆![]() 的离心率是
的离心率是![]() ,
,
可得 ,
,
可解得:
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设点![]() 的坐标分别为
的坐标分别为![]() ,
,
(ⅰ)当直线![]() 斜率不存在时,由题意知,直线方程和曲线方程联立得:
斜率不存在时,由题意知,直线方程和曲线方程联立得:![]() ,
,![]() ,
,
(ⅱ)当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
联立 ,消去
,消去![]() 得:
得:![]() ,
,
由![]() ,有
,有![]() ,
,
由韦达定理得:![]() ,
,![]() ,
,
故![]() ,可得:
,可得:![]() ,
,
可得:![]() ,
,
整理为:![]() ,
,
故有![]() ,
,
化简整理得:![]() ,解得:
,解得:![]() 或
或![]() ,
,
当![]() 时直线
时直线![]() 的方程为
的方程为![]() ,即
,即![]() ,过定点
,过定点![]() 不合题意,
不合题意,
当![]() 时直线
时直线![]() 的方程为
的方程为![]() ,即
,即![]() ,过定点
,过定点![]() ,
,
综上,由(ⅰ)(ⅱ)知,直线![]() 过定点
过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】为维护交通秩序,防范电动自行车被盗,天津市公安局决定,开展二轮电动自行车免费登记、上牌照工作.电动自行车牌照分免费和收费(安装防盗装置)两大类,群众可以 自愿选择安装.已知甲、乙、丙三个不同类型小区的人数分别为15000,15000,20000.交管部门为了解社区居民意愿,现采用分层抽样的方法从中抽取10人进行电话访谈.
(Ⅰ)应从甲小区和丙小区的居民中分别抽取多少人?
(Ⅱ)设从甲小区抽取的居民为![]() ,丙小区抽取的居民为
,丙小区抽取的居民为![]() .现从甲小区和丙小区已抽取的居民中随机抽取2人接受问卷调查.
.现从甲小区和丙小区已抽取的居民中随机抽取2人接受问卷调查.
(ⅰ)试用所给字母列举出所有可能的抽取结果;
(ⅱ)设![]() 为事件“抽取的2人来自不同的小区”,求事件
为事件“抽取的2人来自不同的小区”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴滚动,点
轴滚动,点![]() 恰好经过原点.设顶点
恰好经过原点.设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 有下列判断:①函数
有下列判断:①函数![]() 是偶函数;②对任意的
是偶函数;②对任意的![]() ,都有
,都有![]() ;③函数
;③函数![]() 在区间
在区间![]() 上单调递减;④函数
上单调递减;④函数![]() 的值域是
的值域是![]() ;⑤
;⑤![]() .其中判断正确的序号是__________.
.其中判断正确的序号是__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知sin(-π+θ)+2cos(3π-θ)=0,则![]() ;
;
(2)已知![]() .
.
①化简f(α);
②若f(α)![]() ,且
,且![]() ,求cos α-sin α的值;
,求cos α-sin α的值;
③若![]()
![]() ,求f(α)的值.
,求f(α)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
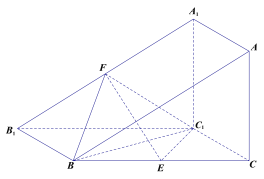
【题目】如图,三棱柱![]() 的侧面
的侧面![]() 是平行四边形,
是平行四边形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 分别是
分别是![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)当侧面![]() 是正方形,且
是正方形,且![]() 时,
时,
(ⅰ)求二面角![]() 的大小;
的大小;
(ⅱ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,指出点
?若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,把函数
)的部分图象如图所示,把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再向下平移1个单位,得到函数
个单位长度,再向下平移1个单位,得到函数![]() 的图像.
的图像.

(1)当![]() 时,求
时,求![]() 的值域
的值域
(2)令![]() ,若对任意
,若对任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com