已知函数f(x)=x|x-2|.
(1)写出f(x)的单调区间;
(2)解不等式f(x)<3;
(3)设a>0,求f(x)在[0,a]上的最大值.
解:(1)函数f(x)=x|x-2|=
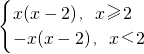
.
∴f(x)的单调递增区间是(-∞,1]和[2,+∞);单调递减区间是[1,2]
(2)f(x)<3等价于
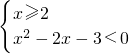
或
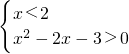
∴2≤x<3或x<2
∴不等式f(x)<3的解集为{x|x<3}
(3)①当0<a<1时,f(x)是[0,a]上的增函数,此时(x)在[0,a]上的最大值是f(a)=a(2-a);
②当1≤a≤2时,f(x)在[0 1]上是增函数,在[1,a]上是减函数,此时f(x)在[0 a]上的最大值是f(1)=1
③当a>2时,令f(a)-f(1)=a(a-2)-1=a2-2a-1>0,解得a>1+

(ⅰ)当2<a≤1+

时,此时f(a)≤f(1),f(x)在[0,a]上的最大值是f(1)=1
(ⅱ)当a>1+

时,此时f(a)>f(1),f(x)在[0,a]上的最大值是f(a)=a(a-2)
综上,当0<a<1时,f(x)在[0,a]上的最大值是a(2-a).
分析:(1)写出函数f(x)=x|x-2|=
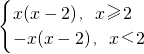
,即可求得f(x)的单调区间;
(2)根据绝对值的几何意义,分类讨论,f(x)<3等价于
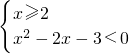
或
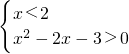
,从而可得不等式f(x)<3的解集;
(3)对参数a分类讨论,确定函数的单调性,从而可求f(x)在[0,a]上的最大值.
点评:本题考查函数的性质,考查解不等式,考查函数的最值,考查分类讨论的数学思想,正确分类是关键.

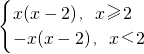 .
.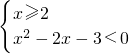 或
或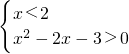

 时,此时f(a)≤f(1),f(x)在[0,a]上的最大值是f(1)=1
时,此时f(a)≤f(1),f(x)在[0,a]上的最大值是f(1)=1 时,此时f(a)>f(1),f(x)在[0,a]上的最大值是f(a)=a(a-2)
时,此时f(a)>f(1),f(x)在[0,a]上的最大值是f(a)=a(a-2)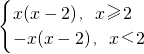 ,即可求得f(x)的单调区间;
,即可求得f(x)的单调区间;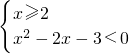 或
或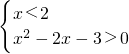 ,从而可得不等式f(x)<3的解集;
,从而可得不等式f(x)<3的解集;

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<