
【题目】已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递减,若f(log2a)+f(2log ![]() a)≥2f(﹣1),则实数a的取值范围是 .
a)≥2f(﹣1),则实数a的取值范围是 .
【答案】[ ![]() ,2]
,2]
【解析】解:函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递减,故f(x)在(﹣∞,0]上单调递增.
若f(log2a)+f(2log ![]() a)≥2f(﹣1),
a)≥2f(﹣1),
即f(log2a)+f(log ![]() a2)≥2f(﹣1),即f(log2a)+f(
a2)≥2f(﹣1),即f(log2a)+f( ![]() a)≥2f(﹣1),
a)≥2f(﹣1),
即f(log2a)+f(﹣log2a)≥2f(﹣1),即f(log2a)+f(log2a)≥2f(﹣1),
即f(log2a)≥f(﹣1)=f(1),﹣1≤log2a≤1,∴ ![]() ≤a≤2,
≤a≤2,
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用奇偶性与单调性的综合的相关知识可以得到问题的答案,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】对于函数f(x)=ax2+2x﹣2a,若方程f(x)=0有相异的两根x1 , x2
(1)若a>0,且x1<1<x2 , 求a的取值范围;
(2)若x1﹣1,x2﹣1同号,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)﹣f(x+2).
(1)求g(x)的解析式及定义域;
(2)求函数g(x)的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意实数a,b定义运算“⊙”:a⊙b= ![]() 设f(x)=2x+1⊙(1﹣x),若函数f(x)与函数g(x)=x2﹣6x在区间(m,m+1)上均为减函数,且m∈{﹣1,0,1,3},则m的值为( )
设f(x)=2x+1⊙(1﹣x),若函数f(x)与函数g(x)=x2﹣6x在区间(m,m+1)上均为减函数,且m∈{﹣1,0,1,3},则m的值为( )
A.0
B.﹣1或0
C.0或1
D.0或1或3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017湖南长沙二模】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
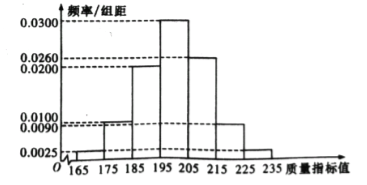
(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017南通二模19】已知函数![]() ,
,![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)求函数![]() 在x
在x![]() 1处的切线方程;
1处的切线方程;
(2)若存在![]()
![]() ,使得
,使得![]() 成立,其中
成立,其中![]() 为常数,
为常数,
求证:![]() ;
;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com