练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人.女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动.
    （1）根据以上数据建立一个 列联表；
    （2）判断性别与休闲方式是否有关系.

    0.05

    0.025

    0.010

    3.841

    5.024

    6.635

    【答案】
    （1）解： 的列联表：

    休闲方式

    性别

    看电视

    运动

    总计

    女

    43

    27

    70

    男

    21

    33

    54

    总计

    64

    60

    124


    （2）解：假设“休闲方式与性别无关”

    因为 ，所以有理由认为假设“休闲方式与性别无关”是不合理的，即有97.5%的把握认为“休闲方式与性别有关”.


    【解析】（1）根据题意将数据填入对应的空格中即可；（2）根据公式K2=计算K2的观测值，然后比较K2与临界值的大小关系.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】我们国家正处于老龄化社会中，老有所依也是政府的民生工程．某市共有户籍人口400万，其中老人（年龄60岁及以上）人数约有66万，为了解老人们的健康状况，政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估，健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级，并以80岁为界限分成两个群体进行 统计，样本分布被制作成如图表：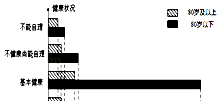
    （1）若采取分层抽样的方法再从样本中的不能自理的老人中抽取16人进一步了解他们的生活状况，则两个群体中各应抽取多少人？
    （2）估算该市80岁及以上长者占全市户籍人口的百分比；
    （3）据统计该市大约有五分之一的户籍老人无固定收入，政府计划为这部分老人每月发 放生活补贴，标准如下：①80岁及以上长者每人每月发放生活补贴200元；②80岁以下 老人每人每月发放生活补贴120元；③不能自理的老人每人每月额外发放生活补贴100 元．试估计政府执行此计划的年度预算．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数 若函数 在 上有3个零点，则 的取值范围为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的各项均为正数，前项和为，且.

    （1）求证：数列是等差数列；

    （2）设，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f （x）=Asin（ωx+φ），（0＜φ＜π）的图象如图所示，若f （x0）=3，x0∈（ ， ），则sinx0的值为（ ）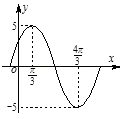
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC中，sin（A﹣B）=sinC﹣sinB，D是边BC的一个三等分点（靠近点B），记 ，则当λ取最大值时，tan∠ACD= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个正四面体的“骰子”（四个面分别标有1，2，3，4四个数字），掷一次“骰子”三个侧面的数字的和为“点数”，连续抛掷“骰子”两次．
    （1）设A为事件“两次掷‘骰子’的点数和为16”，求事件A发生的概率；
    （2）设X为两次掷“骰子”的点数之差的绝对值，求随机变量X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着国家二孩政策的全面放开，为了调查一线城市和非一线城市的二孩生育意愿，某机构用简单随机抽样方法从不同地区调查了100位育龄妇女，结果如表．

    非一线

    一线

    总计

    愿生

    45

    20

    65

    不愿生

    13

    22

    35

    总计

    58

    42

    100

    附表：

    P（K2≥k）

    0.050

    0.010

    0.001

    k

    3.841

    6.635

    10.828

    由K2= 算得，K2= ≈9.616参照附表，得到的正确结论是（ ）
    A.在犯错误的概率不超过0.1%的前提下，认为“生育意愿与城市级别有关”
    B.在犯错误的概率不超过0.1%的前提下，认为“生育意愿与城市级别无关”
    C.有99%以上的把握认为“生育意愿与城市级别有关”
    D.有99%以上的把握认为“生育意愿与城市级别无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，直线C的参数方程为为参数），曲线P在以该直角坐标系的原点O的为极点，x轴的正半轴为极轴的极坐标系下的方程为ρ2﹣4ρcosθ+3=0．
    （1）求直线C的普通方程和曲线P的直角坐标方程；
    （2）设直线C和曲线P的交点为A、B，求|AB|．

    查看答案和解析>>

    同步练习册答案