练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
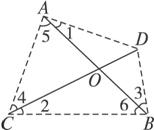
    如图2-27,已知线段AB、CD相交于点O,且OA·OB=OC·OD,求证:A、B、C、D四点共圆.

    图2-27

    证明:连结AC、AD、BC、BD,

    ∵OA·OB=OC·OD,

    ∴.

    ∠AOD=∠COB,∴△AOD∽△COB.

    ∴∠1=∠2.

    同理,可证△AOC∽△BOD,∠3=∠4.

    ∴∠5+∠1+∠6+∠3=∠5+∠2+∠6+∠4=180°,

    即∠CAD+∠CBD=180°.

    ∴A、B、C、D四点共圆.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （1）某工厂准备在仓库的一侧建立一个矩形储料场（如图1），现有50米长的铁丝网，如果用它来围成这个储料场，那么长和宽各是多少时，这个储料场的面积最大？并求出这个最大的面积．
    （2）如图2，已知AB、DE是圆O的直径，AC是弦，AC∥DE，求证CE=EB．
    （3）如图3所示的棱长为a的正方体中：①求CD1和AB所成的角的度数；②求∠B1BD1的正弦值．
    精英家教网

    查看答案和解析>>

    科目：高中数学 来源： 题型：

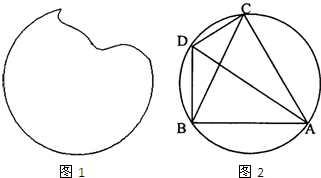    （1）现有一个破损的圆块（如图1），只给出一把带有刻度的直尺和一个量角器，请你设计一种方案，求出这个圆块的直径的长度．
    （2）如图2，已知△ABC三个角，A，B，C满足sin2B+sin2C-sin2A=sinB•sinC，AD是△ABC外接圆直径，CD=2，BD=3，求∠CAB和AD的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）如图1，已知定点F1（-2，0）、F2（2，0），动点N满足|
    ON
    |=1（O为坐标原点），
    F1M
    =2
    NM
    ，
    MP
    =λ
    MF2
    （λ∈R），
    F1M
    •
    PN
    =0，求点P的轨迹方程．
    精英家教网
    （2）如图2，已知椭圆C：
    x2
    4
    +y2=1的上、下顶点分别为A、B，点P在椭圆上，且异于点A、B，直线AP、BP与直线l：y=-2分别交于点M、N，
    （ⅰ）设直线AP、BP的斜率分别为k1、k2，求证：k1•k2为定值；
    （ⅱ）当点P运动时，以MN为直径的圆是否经过定点？请证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (1)如图2-28,已知直线AB过圆心O,交⊙O于A、B,直线AF交⊙O于F(不与B重合),直线l交⊙O于C、D,交AB于E,且与AF垂直,垂足为G,连结AC、AD.

    求证:①∠BAD=∠CAG;

    ②AC·AD=AE·AF.

    (2)在问题(1)中,当直线l向上平行移动,与⊙O相切时,其他条件不变.

    ①请你画出变化后的图形,并对照图2-28标记字母;②问题(1)中的两个结论是否成立?如果成立,请证明;如果不成立,请说明理由.

    图2-28

    查看答案和解析>>

    同步练习册答案