
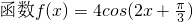 的一个对称中心是
的一个对称中心是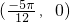
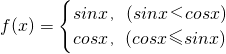 ,那么函数f(x)的值域是
,那么函数f(x)的值域是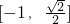
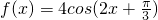 的对称中心,然后判断
的对称中心,然后判断 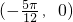 是否为其中之一.
是否为其中之一.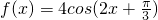 的一个对称中心
的一个对称中心 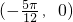 ;
; ,0)(k∈z)
,0)(k∈z) 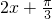 =kπ+
=kπ+
 (k∈z)
(k∈z) 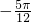
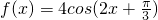 的一个对称中心
的一个对称中心 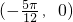 正确.
正确.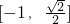 ;
;
 |sin(x-
|sin(x- )|当x-
)|当x- =
= +kπ,x=
+kπ,x= +kπ,即当a=
+kπ,即当a= +kπ时,函数F(x)取到最大值
+kπ时,函数F(x)取到最大值  ,故④错,
,故④错,

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:阅读理解
| π |
| 3 |
| -5π |
| 12 |
|
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•金山区二模)(1)设u、v为实数,证明:u2+v2≥
(2009•金山区二模)(1)设u、v为实数,证明:u2+v2≥| (u+v)2 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| π |
| 3 |
| -5π |
| 12 |
|
| ||
| 2 |
| A..①② | B..③④ | C..①③ | D.②④ |
查看答案和解析>>
科目:高中数学 来源:2009年上海市金山区高考数学二模试卷(理科)(解析版) 题型:解答题
 ;(2)请先阅读下列材料,然后根据要求回答问题.
;(2)请先阅读下列材料,然后根据要求回答问题. .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com