
 能被3整除”的第二步中,
能被3整除”的第二步中, 时,为了使用归纳假设,应将
时,为了使用归纳假设,应将 变形为 从而可以用归纳假设去证明。
变形为 从而可以用归纳假设去证明。 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源:不详 题型:填空题
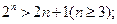
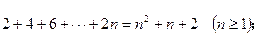
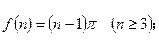
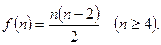
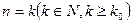 时命题成立,则当n=k+1时命题也成立”,但不满足“当
时命题成立,则当n=k+1时命题也成立”,但不满足“当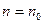 (
(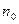 是题中给定的n的初始值)时命题成立”的命题序号是 .
是题中给定的n的初始值)时命题成立”的命题序号是 .查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 设想正方形换成正方体,把截线换成如图的截面,这时从正方
设想正方形换成正方体,把截线换成如图的截面,这时从正方 体上截下三条侧棱两两垂直的三棱
体上截下三条侧棱两两垂直的三棱 锥O—LMN,如果用
锥O—LMN,如果用 表示三个侧面面积,
表示三个侧面面积, 表示截面面积,那么你类比得到的结论是
表示截面面积,那么你类比得到的结论是 
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 个一般的结论:对于
个一般的结论:对于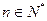 ,12—22+32—42+…+(—1)n+1n2=
,12—22+32—42+…+(—1)n+1n2= 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 .设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥
.设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥 ,若用
,若用 表示三个侧面面积,
表示三个侧面面积, 表示截面面积,你类比得到的结论是 .
表示截面面积,你类比得到的结论是 . 
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
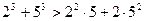 ,
,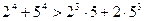 ,
,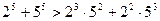 ,…….
,…….查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com