
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() :
: ![]() (
(![]() )的顶点,且椭圆与双曲线的离心率互为倒数.
)的顶点,且椭圆与双曲线的离心率互为倒数.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设动点![]() ,
, ![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,记直线
,记直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(I)双曲线的焦点为![]() ,离心率为
,离心率为![]() ,对于椭圆来说,
,对于椭圆来说, ![]() ,由此求得
,由此求得![]() 和椭圆的方程.(II)设出直线的方程,联立直线的方程和椭圆的方程,利用判别式求得
和椭圆的方程.(II)设出直线的方程,联立直线的方程和椭圆的方程,利用判别式求得![]() 的一个不等关系,利用韦达定理和弦长公式,求得
的一个不等关系,利用韦达定理和弦长公式,求得![]() 一个等量关系,利用
一个等量关系,利用![]() 表示
表示![]() ,进而用基本不等式求得
,进而用基本不等式求得![]() 的最大值.
的最大值.
试题解析:
(Ⅰ)双曲线![]() 的焦点坐标为
的焦点坐标为![]() ,离心率为
,离心率为![]() .
.
因为双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() :
: ![]() (
(![]() )的顶点,且椭圆与双曲线的离心率互为倒数,所以
)的顶点,且椭圆与双曲线的离心率互为倒数,所以![]() ,且
,且![]() ,解得
,解得![]() .
.
故椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)因为![]() ,所以直线
,所以直线![]() 的斜率存在.
的斜率存在.
因为直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,所以可设直线
,所以可设直线![]() 的方程为
的方程为![]() .
.
代入椭圆方程![]() 得
得![]()
![]() .
.
因为![]()
![]()
![]() ,
,
所以![]() .
.
设![]() ,
, ![]() ,
,
根据根与系数的关系得![]() ,
, ![]() .
.
则![]()
![]()
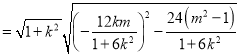 .
.
因为![]() ,即
,即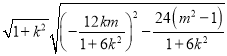
![]() .
.
整理得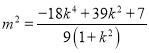 .
.
令![]() ,则
,则![]() .
.
所以![]()
![]()
![]() .
.
等号成立的条件是![]() ,此时
,此时![]() ,
, ![]() 满足
满足![]() ,符合题意.
,符合题意.
故![]() 的最大值为
的最大值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,﹣3),点P的横坐标为14,且 ![]() =λ
=λ ![]() ,点Q是边AB上一点,且
,点Q是边AB上一点,且 ![]()
![]() =0.
=0.
(1)求实数λ的值与点P的坐标;
(2)求点Q的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=8,E是PB上任意一点,△AEC面积的最小值是3.
(Ⅰ)求证:AC⊥DE;
(Ⅱ)求四棱锥P﹣ABCD的体积.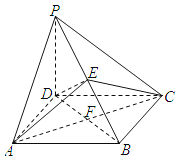
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为 ![]() 米,tanA=
米,tanA= ![]() ,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)
,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)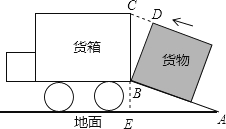
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板两直角边所在直线分别与直线BC、CD交于点M、N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是
(2)如图2,若点O在正方形的中心(即两对角线交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4,是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是 ( )
A. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内一定存在直线平行于平面
内一定存在直线平行于平面![]()
B. 如果平面![]() 不垂直平面
不垂直平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
C. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,那么
,那么![]()
D. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场拟对某商品进行促销,现有两种方案供选择,每种促销方案都需分两个月实施,且每种方案中第一个月与第二个月的销售相互独立.根据以往促销的统计数据,若实施方案1,预计第一个月的销量是促销前的1.2倍和1.5倍的概率分别是0.6和0.4,第二个月的销量是第一个月的1.4倍和1.6倍的概率都是0.5;若实施方案2,预计第一个月的销量是促销前的1.4倍和1.5倍的概率分别是0.7和0.3,第二个月的销量是第一个月的1.2倍和1.6倍的概率分别是0.6和0.4.令![]() 表示实施方案
表示实施方案![]() 的第二个月的销量是促销前销量的倍数.
的第二个月的销量是促销前销量的倍数.
(Ⅰ)求![]() ,
, ![]() 的分布列;
的分布列;
(Ⅱ)不管实施哪种方案, ![]() 与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y=﹣ ![]() +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).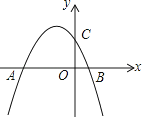
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 的坐标为
的坐标为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,动点
,动点![]() 在圆
在圆![]() 上运动,点
上运动,点![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)求点![]() 的轨迹方程.
的轨迹方程.
(2)过点![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,
, ![]() ,分别与圆
,分别与圆![]() 相切于点
相切于点![]() ,
, ![]() ,求直线
,求直线![]() 的方程,并判断直线
的方程,并判断直线![]() 与点
与点![]() 所在曲线的位置关系.
所在曲线的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com