
 与时间
与时间 (月)的关系:
(月)的关系: ,有以下叙述:① 这个指数函数的底数是2;②第5个月的浮萍的面积就会超过
,有以下叙述:① 这个指数函数的底数是2;②第5个月的浮萍的面积就会超过 ;③浮萍从
;③浮萍从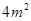 蔓延到
蔓延到 需要经过1.5个月;④浮萍每个月增加的面积都相等;⑤若浮萍蔓延到
需要经过1.5个月;④浮萍每个月增加的面积都相等;⑤若浮萍蔓延到 、
、 、
、 所经过的时间分别为
所经过的时间分别为 ,则
,则 .其中正确的是( )
.其中正确的是( )
| A.①② | B.①②⑤ | C.①②③④ | D.②③④⑤ |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
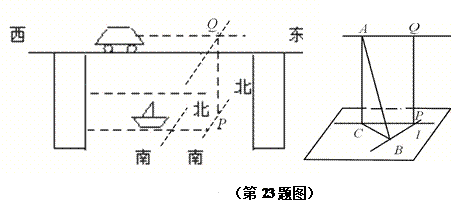
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 本小题满分12分)
本小题满分12分) 00万元利润的目标,准备制定一个激励销售人员的奖励方案:
00万元利润的目标,准备制定一个激励销售人员的奖励方案: (单位:万元)随销售利润
(单位:万元)随销售利润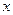 (单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润的
(单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润的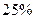 ,现有三个奖励模型:
,现有三个奖励模型: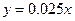 ,
,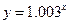 ,
,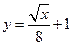 ,问其中是否有模型能完全符合公司的要求?说明理由.(参考数据:
,问其中是否有模型能完全符合公司的要求?说明理由.(参考数据: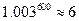 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 3分)
3分)| 运输工具 | 途中速度 (km/h) | 途中费用 (元/km) | 装卸时间 (h) | 装卸费用 (元) |
| 汽车 | 50 | 8 | 2 | 1000 |
| 火车 | 100 | 4 | 4 | 2000 |
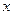 km
km 车运输的总费用分别为
车运输的总费用分别为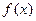 与
与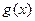 ,求
,求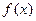 与
与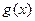 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
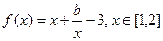
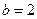 时,求
时,求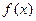 的值域;
的值域;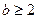 时,
时,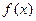 的最大值为M,最小值为m,且满足:
的最大值为M,最小值为m,且满足: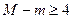 ,求b的取值范围.
,求b的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com