
【题目】已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数)
为参数)
(Ⅰ)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(Ⅱ)若过![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,
,![]() ,求
,求![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某个体户计划经销A,B两种商品,据调查统计,当投资额为x(x≥0)万元时,在经销A,B商品中所获得的收益分别为f(x)万元与g(x)万元,其中f(x)=a(x-1)+2,g(x)=6ln(x+b)(a>0,b>0).已知投资额为零时收益为零.
(1)求a,b的值;
(2)如果该个体户准备投入5万元经销这两种商品,请你帮他制定一个资金投入方案,使他能获得最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若f (x)在区间(-∞,2)上为单调递增函数,求实数a的取值范围;
(2)若a=0,x0<1,设直线y=g(x)为函数f (x)的图象在x=x0处的切线,求证:f (x)≤g(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,没售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了130吨该商品,现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
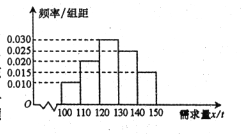
(Ⅰ)视![]() 分布在各区间内的频率为相应的概率,求
分布在各区间内的频率为相应的概率,求![]() ;
;
(Ⅱ)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(Ⅲ)在频率分布直方图的市场需求量分组中,以各组的区间中点值(组中值)代表该组的各个值,并以市场需求量落入该区间的频率作为市场需求量取该组中值的概率(例如![]() ,则取
,则取![]() 的概率等于市场需求量落入
的概率等于市场需求量落入![]() 的频率),求
的频率),求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是二次函数,不等式
是二次函数,不等式![]() <0的解集是(0,5),且
<0的解集是(0,5),且![]() 在区间[-1,4]上的最大值是12.
在区间[-1,4]上的最大值是12.
(1)求![]() 的解析式.
的解析式.
(2)作出二次函数y=![]() 在
在![]() [-1,4]上的图像并求出值域.
[-1,4]上的图像并求出值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】未来创造业对零件的精度要求越来越高.![]() 打印通常是采用数字技术材料打印机来实现的,常在模具制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有发展空间.某制造企业向
打印通常是采用数字技术材料打印机来实现的,常在模具制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有发展空间.某制造企业向![]() 高校
高校![]() 打印实验团队租用一台
打印实验团队租用一台![]() 打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取
打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取![]() 个零件,度量其内径的茎叶图如图(单位:
个零件,度量其内径的茎叶图如图(单位:![]() ).
).

(1)计算平均值![]() 与标准差
与标准差![]() ;
;
(2)假设这台![]() 打印设备打印出品的零件内径
打印设备打印出品的零件内径![]() 服从正态分布
服从正态分布![]() ,该团队到工厂安装调试后,试打了
,该团队到工厂安装调试后,试打了![]() 个零件,度量其内径分别为(单位:
个零件,度量其内径分别为(单位:![]() ):
):![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,试问此打印设备是否需要进一步调试?为什么?
,试问此打印设备是否需要进一步调试?为什么?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com